Area Calculator is an all-in-one calculator that calculates the area of all geometric figures. Based on your selection of the figure, our area calculator will quickly find the area and return the result for you. In addition, you can choose in which square unit you would like to measure it (square meters, square inches, square feet).

Take a look other related calculators, such as:

What is an area in math? Area definition

In math, the number of square unit needed to cover the surface of a closed figure – we call area. As a geometric term, the area is derived from the Latin language in the 1560s, which means “opened or closed surface contained in a defined set of limits”.

If you look around yourself, you will find the use of the area in many situations. Ex. You want to build a swimming pool, or you are unsure what carpet size would be perfect for your room. In all of these cases, you can use the area formula to calculate and find the measures expressed in square feet, square meters, square inches etc..

How to calculate area?

There is a general rule on calculating the area of any shape, so let’s take a look.

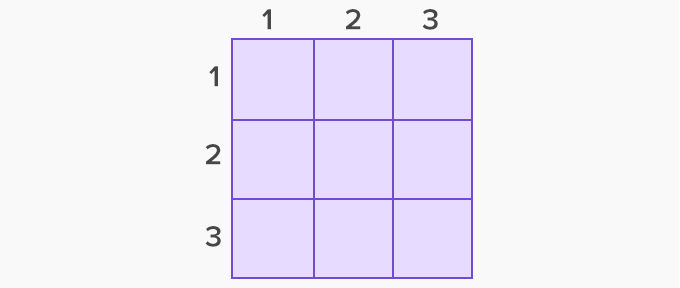
When we want to calculate the area of a particular shape, first, we need to place the shape onto an imaginary grid of which every square in the grid equals 1 square unit.

Example: We want to paint the wall, but we don’t know the area of the wall. First, we imagine that the wall is one huge grid with small squares and all you need to do is count how many of these squares are inside of the grid.

Let’s assume we measure it in square meters, and there is a total of 6 squares in the grid. This number indicates that the area of the wall (how much space is contained inside of the wall) equals 6 square meters.

However, the wall has a rectangle shape, but you may wonder what about circular, polygonal or triangular shapes? How do we calculate their area? We are going to cover all of these aspects in the following sections.

Square area formula

In the previous section, we have explained how the calculation of area works in a nutshell. However, there is no universal formula for all of the shapes. Thus, in this section, let’s find out the formula for calculating the square area.

Square footage of a square = $a^{2}$

We calculate the area of a square by raising the length of one of its sides to two. Why? Because a square has all four sides of equal length.

Method two: In case if the diagonal of a square is known, you can calculate the area without knowing the length of any of its sides using the following formula:

Square area = $d^{2} \div 2$

Raise the length of its diagonal to two and divide the results by 2.

Rectangle area formula

We calculate the area of a rectangle by multiplying the length of its width (shorter side) and length (longer side).

Rectangle area formula = $length \times width$

Method two: If the diagonal of a rectangle is known, then you can calculate the area by only knowing its width and diagonal:

l^{2} = d^{2} - w^{2}

l =\sqrt{d^{2} - w^{2}}

Rectangle area formula = $w \times (\sqrt{d^{2} - w^{2}})$

Triangle area formula

Every triangle has three sides, and in order to calculate its area, we need to know the length of all three sides. This is the basic approach to calculating the area of a triangle:

Triangle area = $1 \div 2 \times b \times h$

b – triangle’s base

h – perpendicular height

It’s important to note that this formula can be used for calculating the area of any type of triangle.

Let’s find out how to find the area of different types of triangles:

Right-Angled Triangle

Triangle area = $1 \div 2 \times Base \times Height$

We see nothing changed; the area formula for right-angled triangles remains the same as the basic formula, and you can read more about it if you head to our Area of a Right Triangle Calculator.

Equilateral Triangle

Triangle area = $\frac{\sqrt{3}}{4 \times side^{2}}$

An equilateral triangle has all three sides equal, so if we are only given the length of at least one of its sides, we can measure the area by the formula above.

Isosceles Triangle

Isosceles triangles have two of their sides equal, so if we know two sides of the triangle, we can calculate the area without knowing the length of the third.

Triangle area = $\frac{1}{4 \times b\sqrt{4a^{2} - b^{2}}}$

Circle area formula

A circle is a bit different shape from the previous geometric figures. A circle does not have sides, bases or height. Instead, we measure it by knowing its radius, diameter or circumference.

We calculate the area of a circle in these 3 ways or use our area calculator:

Knowing the circle’s radius:

Square footage of a circle = $\pi \times r^{2}$

r – the distance between the centre and any point in the circle’s boundary.

Knowing the circle’s diameter:

Area of a circle = $\frac{\pi}{4} \times d^{2}$

d – the line that touches the two endpoints of the circle and passes through the centre.

Knowing the circle’s circumference:

Area of a circle = $\frac{C^{2}}{4\pi}$

C – length of the circle’s boundary

Sector area formula

The sector is a part of a circle. It represents space enclosed by two radii and the angle between them. So the space that a sector takes inside a circle is also considered the area of a sector. Every sector has two types: minor and major. The minor sector is the part less than a semi-circle, as opposed to the major sector, which is greater than a semi-circle.

We calculate the area of a sector through these two possible ways or use our area calculator:

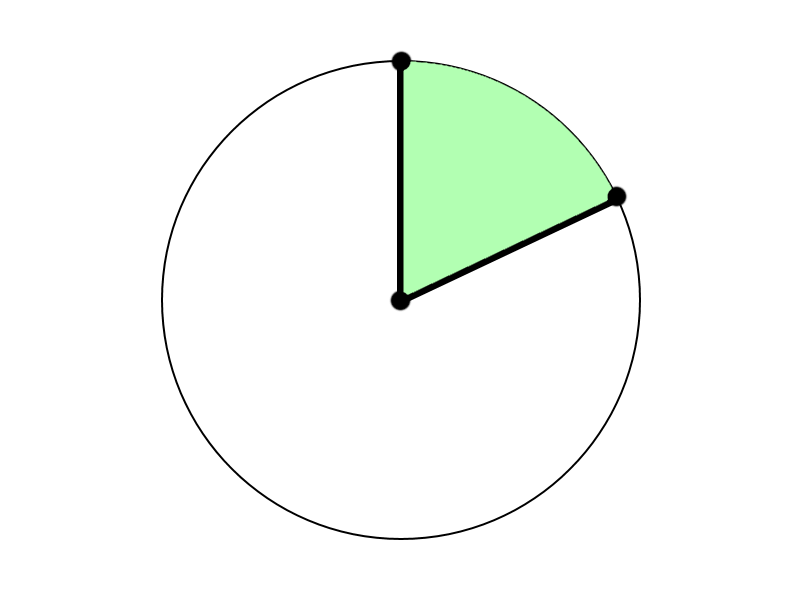
Using degrees:

Square footage of a sector = $\frac{\theta}{360} \times \pi r^{2}$

θ – the angle between two radii

r – radius of the circle

Using radians:

Sector Area = $\frac{1}{2} \times r^{2}\theta$

θ – the angle between two radii

r – radius of the circle

Ellipse area formula

Ellipse is not a perfect circle; thus, the distance from the centre to respective circumferences is not constant. The line connecting two farther points in the ellipse is called the major axis. The line with a smaller distance between two points is called the minor axis. The area of an ellipse can be calculated by multiplying half of the major axis by half of the minor axis.

Square footage of an ellipse = $\pi \times a \times b$

π – PI number

a – major axis

b – minor axis

Trapezoid area formula

In order to find the area of a trapezoid, it’s enough to know the length of two parallel sides and the distance between them (height). There also a calculator for calculating the trapezoid parameters.

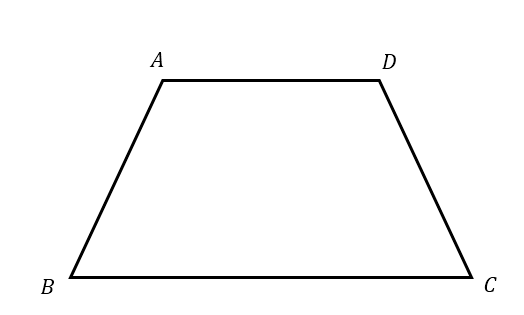
Square footage of a trapezoid = $\frac{1}{2} (a + b) h$

a – base 1

b – base 2

h – the distance between the two bases

Area of a parallelogram formula

A parallelogram is a quadrilateral with two pairs of parallel sides. For example, rhombus, square and rectangle are parallelograms. They all have two pairs of parallel lines that enclose the space and form a geometric figure.

We measure the area of a parallelogram by multiplying the length of its base by its height (altitude):

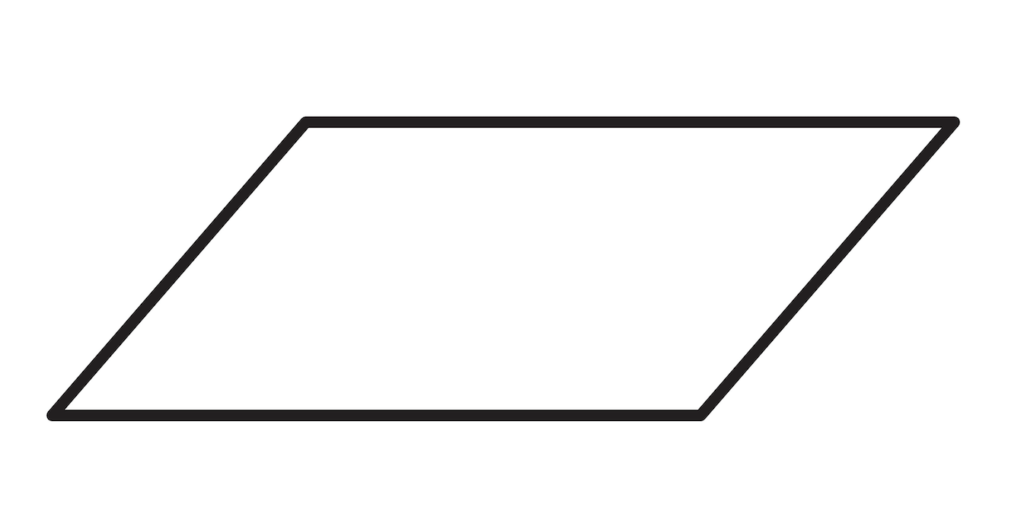
Square footage of a parallelogram = $b \times h$

b – one of its bases

h – the distance between the bases

Method two: You can calculate the parallelogram area using the length of its diagonals:

Parallelogram area = $\frac{1}{2} \times d1 \times d2 \times sin(x)$

d1 – diagonal 1

d2 – diagonal 2

x – an angle between the two diagonals

Area of a rhombus formula

Rhombus is a parallelogram with all equal sides. However, it does differ from a square because the rhombus does not have to have all four right angles between the sides.

We can calculate the area of a rhombus in three different ways or use our area calculator:

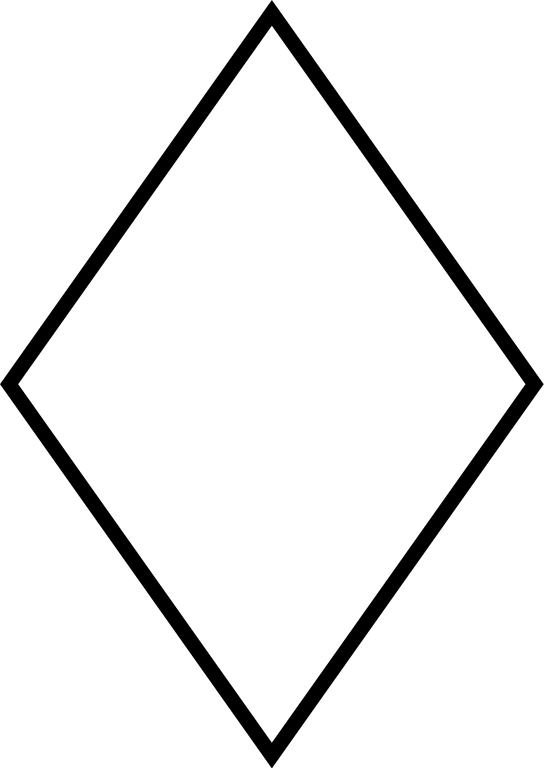
Using the length of the base and height:

Area of a rhombus formula = $b \times h$

b – base

h – height’s length

Through the length of the rhombus’ diagonals:

Rhombus area = $\frac{(d1 \times d2)}{2}$

d1 – diagonal 1

d2 – diagonal 2

Using the length of one side and the angle:

Rhombus area = $side^{2} \times sin(A)$

side – one of the sides of a rhombus (it doesn’t matter which because all of them are equal)

A – an angle between the two sides

Area of a kite formula

Kite is a quadrilateral with four angles, two diagonals and four sides (two pairs of equal adjacent sides). It resembles the rhombus a lot.

There is only one formula for calculating the area of a kite, and it looks the same as the one for rhombus:

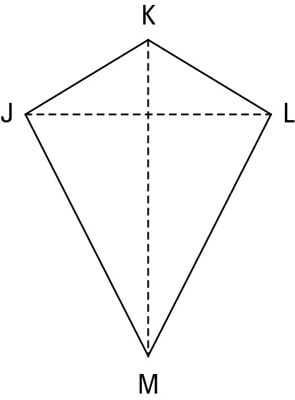
Square footage of a kite = $\frac{1}{2} \times d1 \times d2$

We get the area of a kite by multiplying its two diagonals and dividing that number by 2.

Pentagon area formula

Pentagon is a two-dimensional polygon with 5 sides.

We calculate the area of a pentagon using any of these two formulas or use our area calculator:

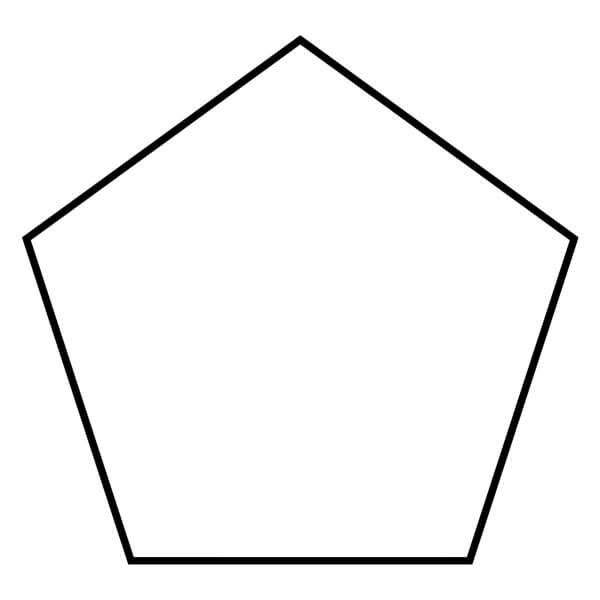
Pentagon area = $\frac{5}{2} \times s \times a$

s – the length of one of the pentagon’s sides

a – apothem (incircle radius)

The area of regular pentagons can also be measured by this alternative formula when only a side is known:

Pentagon area = $\frac{1}{4} \times \sqrt{5} \times (5 + 2\sqrt{5}) \times s^{2}$

Area of a hexagon formula

Hexagon is a two-dimensional polygon with six sides and six angles.

We can calculate the area of a regular hexagon either by knowing its side’s length or using the apothem.

First method:

quare footage of a hexagon = $(3\sqrt{3} \times s^{2}) \div 2$

s – side of the hexagon

Second Method:

Hexagon area = $3 \times a \times s$

a – apothem

s – side of the hexagon

Area of an octagon formula

Octagon is a polygon with 8 sides.

If we want to calculate its area, we first slice it into 8 equal isosceles triangles and then find the area with the following formula:

Square footage of an octagon = $2s^{2} \times (1 + \sqrt{2})$

s – the side of an octagon

Area of an annulus formula

Suppose we draw two concentric circles with the exact centre of different radius. In that case, the two circles will form a shape like a ring which is called an annulus. Since the annulus is based on the radius of both circles, to calculate the area of an annulus, we need to know the area of a smaller and bigger circle. Once we know their areas, we can easily subtract the area of a smaller circle from a bigger circle, and we will get the area of an annulus.

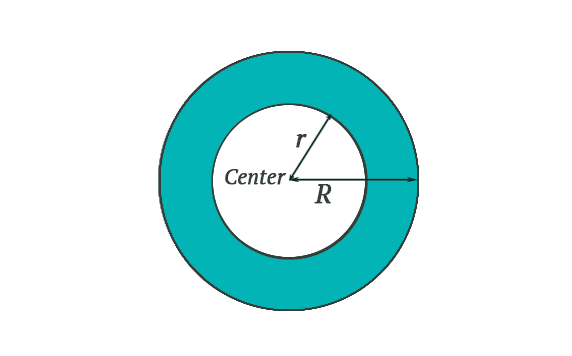
Area of the bigger circle = $\pi R^{2}$

R – radius of the bigger circle

Area of the inner circle = $\pi r^{2}$

r – radius of the smaller circle

Therefore, the area of an annulus is: $\pi (R^{2} - r^{2})$

Area of a quadrilateral formula

A quadrilateral is a closed shape with four lines. If a quadrilateral has all the lines of equal length, we call it a regular quadrilateral. However, if the lines are of different sizes, it is called an irregular quadrilateral.

We can calculate the area of a quadrilateral by dividing it into two triangles:

Square footage of a quadrilateral = $\frac{1}{2} \times d \times$ (Sum of h)

d – one of its diagonals

Sum of h – the sum of all of its heights

Regular polygon area formula

A regular polygon is a polygon with equal sides and angles. For example, these are square, regular pentagon, equilateral triangle and more.

Each of them has a special formula for calculating the area, but this is a universal formula for area of regular polygons:

Regular polygon area = (number of sides × length of one side × apothem) / 2

Also, besides mentioned area calculators, there is another one – Surface Area of a Cone Calculator. Also, we have a general tool for polygons, our Polygon Calculator.

Area Calculator