A more accurate area of a circle calculator will help you get results and calculate the area of a circle using this calculator. You can find all the most important information in this article. About the area of the circular calculator, which formulas we use when calculating, an example that will help you understand it, and much more you can find in the text below.
What is the area of a circle?
The area of a circle is the number of square units required to cover the circle. It is calculated by multiplication the radius squared by π. The area of a circle is the measure of the two-dimensional surface of a circle and is given by the equation:
A = \pi \cdot r^{2}The radius is the distance from the center of the circle to any point on the circumference. A circle is a simple shape, and many math problems involving circles can be solved using this equation.
How to calculate the area of a circle?
There are several ways to calculate the area of a circle. Diameter or radius can calculate the area of a circle.
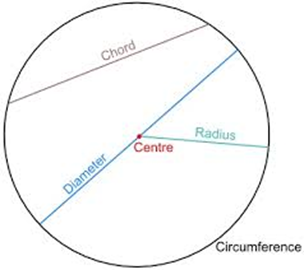
- Diameter can be defined as a line that crosses the middle of a figure and has touched both its margins.
- The radius starts in the very center of the figure and ends on the margin of the same figure.
You can calculate the diameter of the circle by using the radius of the circle by multiplying by 2. The formula for the area of a radius of a circle is:
A = \pi \cdot r^{2}Area of a circle formula (equation)
We learn a formula we can use to calculate the area of a circle. But what is R in this formula?
The letter R represents circles of radius. This is the distance of any line from the middle of the circle to its edge. In geometry, the Greek letter π represents the circumference of the circle used to balance the equation as well as its diameter, which is approximately equal to 3.1416. It is a unique math constant, and you will use this constant in almost every case. To find the solution, that is, to find the area we are looking for regardless of which units of measurement (mm, cm, m, feet, inches, etc.), we use this formula that we have given.
As you have gained enough knowledge and as you now know the formula for the area of a circle, you can try some other calculators that connect the themes of the circle, such as:
How to use the area of a circle calculator?
Diameter to area and radius to the area.
Math defines a circle as a geometric shape with two parts by which we identify them, center and radius (distance from the center to any point on the circle). When we determine the point that will be the center of the circle, and you know how far that point will be from all the points on the circle, you can draw a picture. With a measure of radius, you can say a lot about a circle: what is its diameter, what is its circumference, and what is the area of the circle.
With our calculator, you can quickly get results and calculate the area of a circle, diameter, and radius. The first thing you need to do is determine what it is about whether the value refers to the diameter or the radius using the image you have below, as well as the definition and formula we mentioned at the beginning. Then you enter the appropriate value in the calculator field, and your result is there.
Why do we need the surface area of a circle calculator?
When drawing a circle, the length of the radius is essential for calculating the area. But if you are drawing a circle by hand, it cannot be easy to measure the radius. The Surface Area of a Circle Calculator can help you calculate the area of a circle. It is a simple calculator that provides the surface area of a circle, given the radius. It is helpful for people drawing circles by hand but wants to make sure they are calculating the area correctly.
We define a circle as a three-dimensional object that has no edges. The distance from the center to the inner circle, we find the radius. How can we explain the area of a circle? It is necessary to know the number of square units that can fit inside a circle if each square within the same circle has an area of 1 cm2. Our calculator can help you calculate the area of a circle by knowing the value of the radius.
Example: find the area of a circle
Through the article, we learned the definition of a circle and the formula we need to calculate the area of a circle, and now we will apply it to the task.
If the radius is 9 cm, how do we calculate the area of the circle? We will enter the amount of radius into our formula with the amount of radius we have:
r = 9cm
A=?
Area of a circle units
The units of measurement that we can use when calculating the area of a circle are as follows:

Practical application
It is not possible to measure the circumference of diameter or radius in some situations. If we do not identify the diameter or draw it, it cannot be easy to approximate the circle’s center. For specific processes such as a pizza pan – you can use a measuring tape and measure the circumference more accurately than measuring the diameter.
If we look around, we see that we are surrounded by various objects such as a food plate, a can, a traffic cone, and we can say that they all have the surface of their circle. The volume and surface can be taken as a prime because it also has a three-dimensional shape. Architects often use the properties of a circle because they are symmetrical when designing parks, buildings, roundabouts, panoramic points, and the like. The circle is irreplaceable in the work of artists and painters. Engineers use symmetrical properties of the circle, which we can see when making cars, watches, bicycles, carts, etc. The development of the invention of the circular wheel led to the progress of civilization.
FAQ?
1. What is the formula for the area of a circle?
The formula of the area of a circle is A = π*r
2. How to find the area of a circle using diameter?
The diameter of the circle is double the radius of the circle. Hence the area of the circle formula using the diameter is equal to π /4 times the square of the circle’s diameter. The formula for the area of the circle, using the diameter of the circle π /4 * diameter2.
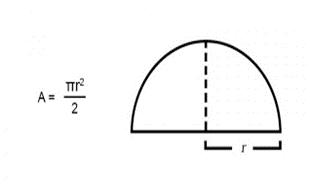
3. How do you find the area of a half-circle?
The area of a semicircle can be calculated using the length of radius or diameter of the semicircle. The formula to calculate the area of the semicircle is: Area = πr2/2 = πd2/8, where ‘r’ is the radius, and ‘d’ is the diameter.
4. What is the area of a 12-inch circle?
If 12” is the circle’s diameter, the area is π * (12/2)2 = 113.097 square inches.
