Here you can use our Area of the Right Triangle Calculator (ART) to calculate the area of the Right Triangle. CalCon mobile app or browser interactive user face allows you to find the area using an interactive calculator. You have to choose which variation of the given values you have and then enter them in the marked fields. As a result, the area of the right triangle is presented in the marked field.
The following text will show what a right triangle is and which formulas we can use to calculate its area. Furthermore, we will explain what an isosceles right triangle is and various variations of formulas. Finally, we will show a concrete application of our calculator with a few examples.
While you are here, you should look at some more of our solutions and help calculate various math quantities, such as Root or Cube. Also check other in math section.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is the Right Triangle?
In each triangle, only one angle can be right. So, for example, if this triangle ABC had two 90 degrees angles, then at point C, there would be two normals on line a.
The definition of the right triangle is as follows:
A triangles with one 90 degrees angle are called a right triangles. This is because of the opposite length, the right angle is the hypotenuse, and the other two sides are the cathetus.
In a right triangle, the hypotenuse is larger than each cathetus. Therefore, the legs or catheti are also two heights of the triangle.
The Pythagorean theorem holds in a right triangle. Pythagoras’ theorem is the relationship in Euclidean geometry between the three sides of a right triangle.
Pythagorean theorem:
If the triangle is right-angled, then the sum of the squares over the legs is equal to the square over the hypotenuse.
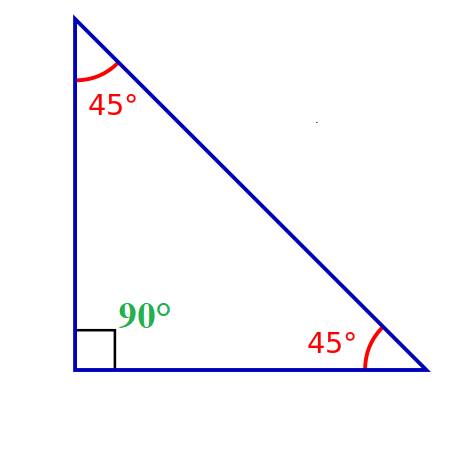
Area of Right Triangle formulas
The simplest formula for calculating the area of this triangle is to multiply the value of the legs and divide them by two:
P = \frac {a \cdot b}{2}where
P – area in square units
a – one leg/cathetus
b – second leg/cathetus
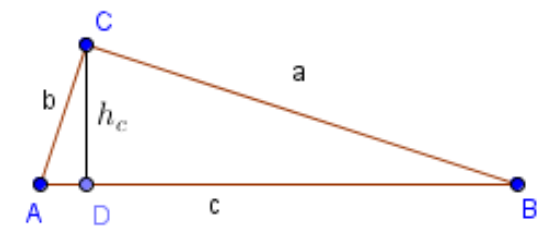
The previous formula is derived from the general formula for calculating the area of any triangle, and it reads:
P = \frac {1} {2} \cdot a \cdot b \cdot \sin(between \; angle)If we take into account that the angle between the sides a and b is equal to 90 degrees, and the sine of 90 degrees is 1, so that the formula gets a simpler look, i.e.:
P = \frac {a \cdot b}{2}A right triangle is a triangle to which the well-known Pythagorean theorem is applied when it is required to find the length of the leg or hypotenuse.
A triangle that is rectangular and whose sides are in the ratio of 3 to 4 to 5 is called the Egyptian triangle.
Heron’s formula
Heron’s pattern, named after the Alexandrian mathematician and engineer Heron about 2,000 years ago, is used to calculate the area known to be three sides long in the triangle. The semicircle (half of the perimeter) is used in the equation:
S = \frac {a+b+c}{2}Heron’s equation is given below:
P = \sqrt {s\cdot (s-a)\cdot (s-b) \cdot (s-c)}Area of an Isosceles Right Triangle
An isosceles triangle has two equal sides. These two equal sides are marked with a small Latin letter b and are called the arms of an isosceles triangle. The side above which the arms are located is called the base and is marked with the lowercase Latin letter a. The vertex C opposite the base is called the top of an isosceles triangle.
A special case is when we have an isosceles triangle whose angle is 90 degrees. Such a triangle is called an isosceles right triangle.
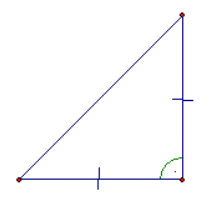
Since the two legs coincide, we will denote them both by the small Latin letter a and the hypotenuse by c. When we replace both letters in Pythagoras’ theorem, we get:
c^2 = a^2+a^2
c^2 = 2 \cdot a^2
c = \sqrt {2 \cdot a^2}c = a \cdot \sqrt {2}From this, we can conclude that the hypotenuse length is equal to the leg size multiplied by √2. Therefore, we need only one of the three lengths to determine the other two sides of an isosceles right triangle.
Calculation of this math form is even simpler, so the formula will be:
P = \frac {a^2} {2}Area of Right Triangle With Hypotenuse
If we consider Pythagoras’ theorem:
c^2 = base^2+height^2
However, although it is impossible to find the area of a right triangle with only the hypotenuse, it is possible to find the area if we know another size, one of the base or height. Here is the formula with height:
P = \frac {c \cdot h} {2}How to use the ART calculator?
So, as far as our calculator is concerned, it is possible to find the desired value in two ways depending on whether you have two available lengths or one length and one angle.
Suppose you know two lengths, i.e. two legs or one leg and the hypotenuse. In that case, you need to enter them in the provided fields (a, b, c), then the remaining values will be automatically calculated in the selected units.
If you have one length and one angle, then select the angle and one side mode, in which you will enter the measures in the provided fields. When you enter what you have, the other fields will be filled in automatically, and the area will be shown below, also in the selected units of measure.
Area of Right Triangle Examples
Below we will show some examples of calculations with different given values. We will use our ART calculator for calculation.
Example 1: Given two sides
Suppose we have given two legs, the first 10 meters long and the second 8 meters long. We will select a two-length mode for the calculation so that we will make an entry:
- Enter 10 in field a
- Enter 8 in field b
- Field c is automatically filled and is 12.81 m
- The area is 40.03 m2
Example 2: Given one side and one angle
We have the length of one leg, let’s say, and it is 5 centimetres. So the angle that this leg closes is 35 degrees.
- First, we change the units of measurement from meters to centimetres and enter the value 5 in field a
- Then it is necessary to enter the angle in units of degree by entering the value 35 in the field Angle α
- We will automatically get the second leg and angle, and it will be 7.14 cm and 55 degrees.
- The hypotenuse is 8.72 cm, and finally
- The area is 17.85 cm2
Remember to change the units of measure to get everything in the same. If you have trouble with understanding of angles, then you should read this post about conversion of angles.
Example 3: With hypotenuse
If we have a length of the hypotenuse and one cathetus, you have to enter these values in given fields, so let’s assume we have one cathetus, which is 4 meters, and a hypotenuse is 5 meters.
- Enter cathetus in field a
- Enter 5 in field c
- The calculated value of other cathetus is 3 meters,
- P is 6 square meters.
FAQ
What is the Area of a Right Triangle?
The area of a right triangle is the total area of the space or area covered by the 90° triangle. It is expressed in square units (square meters, centimetres, etc.).
What are the Isosceles 90° Triangles?
It’s the math form where you have one angle of 90 degrees and the same lengths of legs. This is also 45-45-90 triangle.
