Condense Logarithms Calculator is a condensing logarithms step-by-step calculator. Besides other online calculators, our Condense Logarithms Calculator provides a simple way to add, subtract and raise logs to a particular exponent. With this useful tool, just enter log properties: the base and exponent. Then, our calculator will solve the equation according to the formula you choose.
Also, you can learn about trigonometric functions and their use in geometry, 45 45 90 triangle calculator, 30 60 90 triangle calculator. For more geometry and trigonometry related posts and questions, as well as other math articles, explore our database of different calculators like sum and difference identities, Cofunction Calculator, Phase Shift Calculator and find your answer.
Take a look other related calculators, such as:
- Power reducing formula calculator
- Probability calculator 3 events
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
- Perimeter Calculator
What is a logarithm – definition?
A logarithm is a math expression that tells us which power we need to raise a particular number, “a” to get a number “b”. It is an inverse function of exponents. In terms of math problems, logs are very useful in solving them. Thus, if you want to have basic math skills, you should definitely know them. However, everybody hears about this math concept in high school (algebra), if not even earlier. In algebra, you learn about logarithmic functions. For example, let’s look at the example below:
3 \times 3 \times 3 = 27 -> We need to multiply the number of 3 three times by itself to get 27.
So, the log is 3, and we write it down this way:
Logarithmic expressions does not have only one log property, but three specific properties you should know:
- base (a number that we multiply by the answer number)
- argument (a number that we get)
- and answer (how many times we need to multiply the base to get the argument)
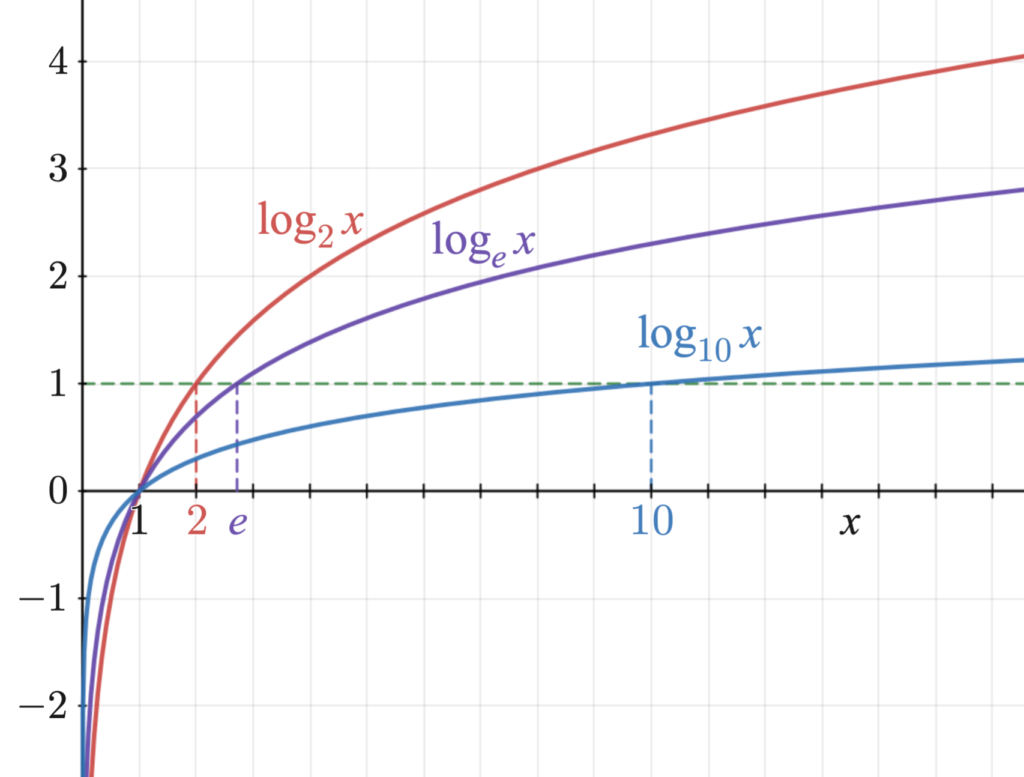
Base 10 logarithms
Sometimes, if you see a logarithmic expression without a base, it means that the base is 10. Simply, we do not explicitly write it.
For example: \log(100) – we can also write as \log_{10} (100) = 2
Base e logarithms
Logarithms with basis “e” is often called the natural logarithm. They have the basis of Euler’s number, which equals around 2.71828.
For example: \ln(100) – we can write as \log_e (100) = 4.6
How to rewrite logarithms?
We already mentioned that logarithmic and exponential functions are inverse to each other. In terms of their connectedness, we can take logarithmic expressions and convert them into exponential ones. How? Let me show you:
For example, y = \log_a x is the same as if we write x = b^{y}

You still confused or don’t believe me? I will show you a few real examples below:
\log_3 (27) = 3
27 = 3^{3}
or vice-versa
10^{3} = 1000
3 = \log_{10} (1000)
How to condense logarithms?
Condensing or simplifying logs, you need to know the three most common rules in the following log definition:
The log of an exponent:
Suppose we have a log and multiplication number before it to calculate that equation. In that case, we take that number and raise the exponent of the log to it. Let’s see how to do it:
x \times \log_n a = \log_n a^{x}
Addition of logs with multiples:
x \times \log_n (a) + y \times \log_n (b) = \log_n (a^{x}) + \log_n(b^{y}) = \log_n (a^{x} \times b^{y})
When we have two logs with multiples, and we need to add them, the first step is to take the multiplication number and solve each log using the log of an exponent approach, as we explained above. Once we get rid of multiples, now we have two logs of the equal base, and we need to add them. You can rewrite the expression as one single log of their multiplication to add them.
Subtraction of logs with multiples:
x \times \log_n (a) - y \times \log_n (b) = \log_n (a^{x}) - \log_n (b^{y}) = \log_n (a^{x} \div b^{y})
The difference between two logs is almost identical to when we add them. Therefore, we start by getting rid of multiples and raising the exponents of logs to their power. Then, we rewrite the logs and write it as a log of their division – log of the quotient.
Condense the logarithmic expression
In the previous part, we explained three simple formulas that we can use to simplify or condense logs. In this part, we will use the mentioned formulas and apply them in the precalculus (algebra) examples.
Example for Logarithm of an exponent:
3 \times \log_3 (9) = \log_3 (9^{3}) = \log_3 (729) = 6
Example for Addition of logs with multiples:
2 \times \log_2 (100) + 4 \times log_2 (4) = \log_2 (100^{2}) + \log_2 (4^{4}) = \log_2 (10000 \times 256) = \log_2 (2560000) = 21.28
Example for Subtraction of logs with multiples:
4 \times \log_2 (4) - 1 \times \log_2 (16) = \log_2 (4^{4}) - \log_2 (16^{1}) = \log_2 (256 \div 16) = 16
Example: using the condense logarithms calculator
We showed you the formulas, but wait! Solving the logarithmic expressions all by yourself can be tedious and time-consuming. Therefore, instead, you can use our condense logarithms calculator to simplify and calculate the log. Our calculator supports all three formulas we mentioned in the previous parts. In addition, you can either add or find the difference of logarithms and calculate “number times log” expressions.
Let’s use the calculator and calculate the number times log equation:
Steps:
- Enter the variables (x – given value of a number, n – given base, a – given exponent)
- Suppose we have 3 \times \log_3 (8)
- The calculator will use the entered variables and give you the result, which is: 5.67
Adding logarithms
If we have two logs with the same base and we want to add them – multiply their exponents:
\log_a (b) + \log_a (c) = \log_a (b \times c)
Subtracting logarithms
Subtraction of two logs with the same base is done by dividing their exponents:
\log_a (b) - \log_a (c) = \log_a (b \div c)
A number times log expression
In expressions of the logarithm of a product and a number, we can calculate them by firstly moving the multiple from the left side of the expression and raising the exponent to the power of that multiple. This way, you can easily solve the expression and get the result of the logarithm:
c \times \log_a (b) = \log_a (b^{c})
FAQ
How do you condense a logarithm?
Condensing a logarithm can be done using one of the three available formulas:
The logarithm of an exponent:
We take the number before the logarithm and raise the exponent of the logarithm to its power.
Addition of logarithms with multiples:
The first step is to take the multiple and solve each logarithm using the log of an exponent approach, as we explained above. Once we get rid of multiples, now we have two logs of the equal basis, and we need to add them. You can rewrite the expression as one single logarithm of their multiplication to add them.
Subtraction of logarithms with multiples:
We start by getting rid of multiples raising the exponents of logarithms to them. Then, we rewrite the logs and write it as a log of their division – logarithm of the quotient.
2. How do you expand logarithms step by step?
Expanding logarithms is the opposite process of condensing them. In an expansion of logs, we take the logarithmic expression and divide it into several smaller components. There are some expanding formulas we need to follow when you expand a logarithm:
Product Rule:
\log_b (M \times N) = \log_b (M) + \log_b (N)Quotient Rule:
\log_b (M \div N) = \log_b (M) - \log_b (N)Power Rule:
\log_b (M^{K}) = k \times \log_b (M)Zero Rule:
\log_b (1) = 0Identity Rule:
\log_b (b) = 1Log of Exponent Rule:
\log_b (b^{k}) = kAn exponent of Log Rule:
b^{\log_b (k)} = k