30 60 90 Triangle Calculator

You form a triangle as a geometric shape with three sides and three corners. The ratio of angles tells us what kind of triangle it is. In addition to the 45 45 90 triangle calculator, this calculator you can use to calculate 30 60 90 triangles. When we talk about calculators as tools, they greatly facilitate checking the accuracy of calculations. So, if you want to find out more about what this new calculator brings and what formulas you can use, check out below.

Also, suppose you seek to enlarge your knowledge. In that case, even more, you shouldn’t miss using these calculators too: Trigonometry calculator, Distance between two parallel lines, Segment addition calculator, Rip Rap Calculator and Phase Shift Calculator.

Take a look other related calculators, such as:

• Power reducing formula calculator
• Probability calculator 3 events
• Cofunction calculator
• Sum and difference identities calculator
• Fundamental counting principle calculator
• Condensing logarithms calculator
• Population density calculator

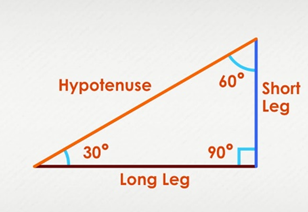
30 60 90 right triangle theorem

We can define three fundamental properties and characteristics to understand the triangle theorem 30-60-90. These properties are also explicitly described for right triangles. The first property states that the longest side of a triangle called the hypotenuse in practice, always has a value twice as long as the shorter leg. You can also calculate the value of the length of the longer leg multiplying the value of the shorter leg by the root number 3. And, if you know the values of any page 30-60-90 of the triangle, it will help you find the unknown sides’ values.

You can mark the value of the shorter leg with y, the value of the hypotenuse 2y, while the value of the longer leg is:

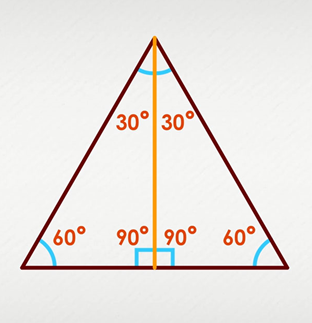
y\cdot \sqrt{3}

We can emphasize that all triangles 30-60-90 are similar and that two such triangles that share one long leg thus form an equilateral triangle. Interesting, isn’t it?

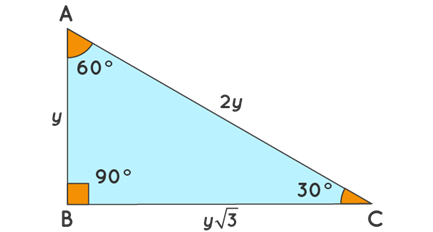
The figure below shows an example of a right triangle 30-60-90, whose side lengths should always be with each other. Triangle ABC, has angle C = 30 degrees, angle A = 60 degrees and angle B = 90 degrees. The side of the triangle is opposite to the angle of 30 degrees, AB = y, and it as such is called a short leg because it is also the shortest. The side opposite the angle of 60 degrees marked BC = y√3 is called the long leg of the triangle, and it is the middle side in length. At the same time, the remaining side of the triangle is also the longest marked AC = 2y, known as the hypotenuse.

30 60 90 triangle ratio

When determining the 30-60-90 triangle theorem it is essential to know the ratio of the sides of the triangle 30-60-90. Since this is a particular type of right triangle, you must always align the lengths of the sides of the triangle, so the ratio of 30-60-90 triangles has the following appearance:

for sides

1 : √3 : 2 = (y : y√3 : 2y)

or for angles

1 : 2 : 3 = (30° : 60° : 90°)

30 60 90 triangle formula

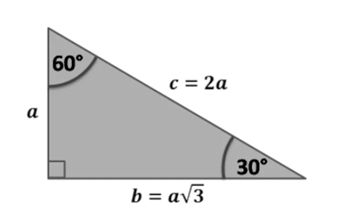
From the geometric point of view, the formula used for the calculation lies in the basics of trigonometry. If we want to calculate page lengths, we can use a sine angle of 30 degrees. According to the attached graph, we can calculate the value of the lengths of pages b and c using several formulas:

\frac{a}{c} = sin30 = \frac{1}{2}

where c = 2a

\frac{b}{c} = sin60 = \frac{\sqrt{3}}{2}

where b = c√3/2

30 60 90 triangle rules and properties

When it comes to the rules you can apply in the 30-60-90 triangle, you will probably manipulate the values of the hypotenuse and the shorter legs of the triangle. The geometry is behind all these links and connections between all three sides of the triangle, and you can see what it looks like in the table below:

If you know…	Then…	To get…
Hypotenuse	Divide by 2	Short leg
Short leg	Multiply by 2	Hypotenuse
Short leg	Multiply by √3	Long leg
Long leg	Divide by √3	Short leg

When following the properties and rules, you can lose sight of the fact that it is still a triangle. It would help if you never forgot that the shape of a triangle is constant in all conditions. Therefore, internal angles should be added up to 180 degrees, while the sides should be following the rules of Pythagoras theorem:

a^{2} + b^{2} = c^{2}

How do we solve a 30 60 90 triangle? – example

 Let us give you more detailed explanations for the formulas for calculating each of the cases listed below, and then we will apply those same formulas to one case study.

Solve Leg A

If you need the formula to calculate the value of the length of leg A, then we can rely on the value of leg b following the following expression:

a = \frac{b\cdot \sqrt{3}}{3}

Solve Leg B

After that, you need to calculate the length of leg B using a formula that looks like this:

b = a \sqrt{3}

Calculate the Hypotenuse

Following the previous explanations and rules related to the longest side of the 30-60-90 triangle, the hypotenuse.
The formula for calculating the hypotenuse has an effortless appearance:

c = 2 \cdot a

Area of a 30-60-90 Triangle

The basic formula for calculating the area of any two-dimensional shape is the number of square units you need to fill the space within that shape. In the case of 30-60-90 triangles, the formula you can use to calculate the area of a triangle is:

A = \frac{1}{2}\cdot b\cdot h

where the values are:

A = triangle area
b = base of the triangle
x = height of the triangle

Calculate Perimeter

When calculating the perimeter of a triangle of any shape, we need to have the sum of the edges. Therefore, the perimeter of the 30-60-90 triangle is equal to the sum of the sides and the hypotenuse. It looks like this:

P = a + b + c

Example:

Now, when you are familiar with all the rules, formulas, and definitions, you can apply this to the following task:

Find the value of the length of the hypnotic of a right triangle if the value of one side is 8 and the other is 8√3.

8: 8√3 = 1: 1√3

From this mathematical expression, we conclude that it was 30-60-90. Therefore, we know that the hypotenuse length is equal to the product of the value of the minor page with the number 2. The conclusion is that the hypotenuse value in this example is equal to 16.

You can use our calculator to facilitate the calculation process, which works on an elementary principal. After accessing our calculator, you will see special blank name fields. Whatever value you enter, whether side a, side b, or triangle area, the calculator will display the results for other empty fields.

30 60 90 triangle proof

To prove the relationships in a 30-60-90 triangle, we need to use trigonometry and the properties of similar triangles.

Let’s start by drawing a 30-60-90 triangle ABC, where the side opposite the 30-degree angle is labeled “a,” the side opposite the 60-degree angle is labeled “b,” and the hypotenuse is labeled “c.”

Using the Pythagorean theorem, we know that:

c^2 = a^2 + b^2

We can also use the properties of similar triangles to determine the relationship between the sides of a 30-60-90 triangle. Specifically, we know that if we draw an altitude from the vertex of the 60-degree angle to the opposite side, it will divide the triangle into two smaller triangles that are similar to the original triangle.

Let’s call the altitude AD, where D is the point on side BC that the altitude intersects. Because triangle ABC is a 30-60-90 triangle, we know that angle ABD is 30 degrees and angle ACD is 60 degrees. Therefore, triangle ABD is a 30-60-90 triangle as well.

Using the properties of similar triangles, we can say that:

\frac{AD}{AB} = \frac{AB}{AC}

Simplifying this equation, we get:

AD = AB^2/AC

Since triangle ABD is a 30-60-90 triangle, we know that BD = AB/2. Therefore, we can substitute BD for AB/2 in the above equation:

AD = (2BD)^2/AC AD = 4BD^2/AC

Now, let’s look at triangle ACD. We know that angle ACD is 60 degrees, so the relationship between its sides is:

AC = 2AD

Substituting our expression for AD from the previous equation, we get:

AC = 2(4BD^2/AC) AC^2 = 8BD^2

Substituting BD for AB/2 and simplifying, we get:

AC^2 = 3AB^2

Using the Pythagorean theorem, we can also say that:

AC^2 = c^2 AB^2 = a^2 BD^2 = b^2/4

Substituting these equations into our previous equation, we get:

c^2 = 3a^2 b^2 = (a^2)/3 c = 2a√3

Therefore, we have proven the relationships in a 30-60-90 triangle:

• The hypotenuse is twice the length of the shorter leg and √3 times the length of the longer leg.
• The longer leg is √3 times the length of the shorter leg.

FAQ?