This Segment Addition Postulate Calculator can help you apply this feature in the process of summing the lengths of two adjacent segments that ultimately result in the value of the total segment. Based on a detailed analysis and research of this topic, you can find out below about the definitions, how the calculator works, and its application, with good examples that will support all formulations.
Geometry can be fun with our calculators. So, check the other math calculators like the Trigonometry Calculator or Geometric Mean and solve your geometry problems. On the other hand, if you like to play with numbers, make sure to see other posts on this site, such as Sig Fig, or maybe you want to express numbers in Scientific Notation, or just deal with logarithmic numbers or 30 60 90 triangle, everything is available in our math database.
Take a look other related calculators, such as:
- Phase shift calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is a Segment?
It is necessary first to define the term line. It represents an infinite direction or set of points that extend in both directions. Since geometry is a science that studies lines, you can add an arrow at the end to draw lines to show its infinity. If we want to offer a line segment when drawing lines, you can put two dots instead of arrows. A segment in math and geometry is a part of a line with a fixed length and two endpoints.
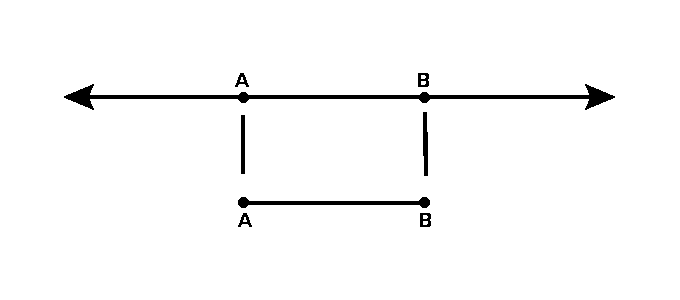
The main difference between a line and a segment is how it symbolizes and because it is not infinite but has a precisely defined length. You can measure the segment length value in metric units such as centimeters, millimeters, feet, or inches.
Segment Bisector – Definition and types
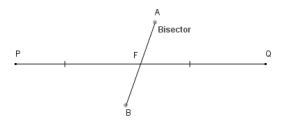
In fact, the human eye can quickly and accurately visually divide things into two equal, symmetrical parts. When we talk about the bisector of a line segment, it denotes the intersection of the segment into two halves or pieces. A bisector can be in the form of a point, direction, ray, or segment line that will intersect another segment line.
The fundamental characteristic of the bisector is that it always passes through the central part of the segment, dividing it into two parts. It can be vertical, and if it is a bisector in the form of a ray or a direction, it will have infinity.
Types
You can use a point as a place in space that has neither shape nor size. It marks the beginning or end of drawing a figure. They can be collinear and coplanar. When we use a point as the bisector of a segment, it divides the line into two equal parts and is called the midpoint.
The line represents a series of points that go to infinity. It has no thickness, and you can stretch it in both directions. We distinguish several types of lines. We know parallel lines, vertical lines, and horizontal lines. Those that intersect at an angle of 90 degrees are called perpendicular lines.
Unlike a line, a ray has a fixed starting point, and its end is not defined. In everyday life, you can see this example in the form of sunlight or light emitted by a torch. You can present it with an arrow symbol.
The bisector can also be in the form of a segment line. That means it must have a defined length, as shown in the figure below. As such, it represents the distance between two endpoints of a segment, which you can measure.
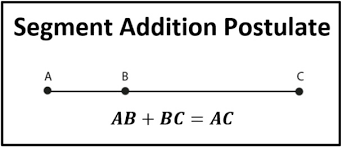
Segment Addition Postulate – Definition
If you have some two points, A and C, positioned on a line segment, you can place the third point B on the line segment between points A and C. You can do it only if the sum of the distances of points A and B and the distance of points B and C is equal to the total length from point A to point C.
Also, you can apply this math postulate if you have set values of endpoints and arbitrary third points positioned somewhere on the segment line.
Suppose you pay attention to the name “segment addition postulate” in detail. In that case, you can conclude that the emphasis on applying this is exclusively on the segment line. In contrast, the “addition” section denotes the essential operation of summing point distance values.
Segment Addition Postulate Formula
Based on the definition of the postulate, it is effortless to formulate a definition that follows the theoretical background. This is the basic addition operation, and in this case, it looks like this:
AB + BC = AC
The designations refer to the distance values, respectively, between points A and B, B and C, and A and C.
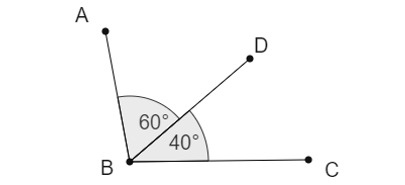
Segment vs Angle Addition Postulate
For the sake of comparison, we will take the angle addition postulate as an example. The definition of this one tells you that when you place two or more angles next to each other in such a way that their vertices are common, the sum of these adjacent angles is equal to the total sum of the angles.
For instance, the sum of the resulting angle. To apply this, you need to place the corner points next to each other. The main difference between these postulates is that the first one considers the lines. On the other hand, the second deals with the relationship of angles.
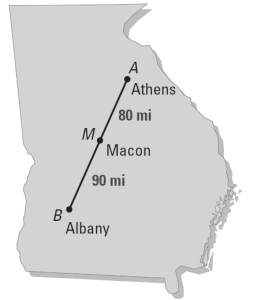
Segment Addition Postulate Calculator – Example
In this case, our Segment Addition Postulate Calculator will help you with all the necessary measurements. It calculates the length of the segment line using a formula you probably already know. We will take as an example that you know the value of the distance of points A and B. The distance is 20 cm. Considering that point B is a bisector of the segment line, conclude that the distance of points B and C is also equal to 20 cm.
In the end, the distance of points A and C is equal to the sum of the previous lengths. By entering all of the above, you can get the same values as we stated. It is up to you to try and see for yourself.
Segment Addition Postulate Calculator: Real-World Usage
So, the importance of knowing and recognizing segments and angles in the space around us is enormous, and can solve your everyday life problems. As for the daily application of the segment addition postulate is diverse, from architecture, construction workers, and engineers to you who want to measure the remaining distance to the desired destination.
For instance, you can apply the math rule of postulate in the situation of sharing a sandwich or cake with loved ones into an equal number of parts so that everyone can enjoy it together.
FAQ
What is a segment addition postulate?
In geometry, you can define this as an axiom that says that when you divide a segment into several parts, the sum of the values of the lengths of the components is equal to the total length of the segment.
How do you find the midpoint of a segment?
If you are in a situation where you want to divide a line segment into two equal parts, then you will need to know the midpoint. It represents the intersection point. To find the midpoint, you need to enter the data in the following math formulas (x_1 + x_2) \div 2 \; \text {and} \; (y_1 +y_2) \div 2 , creating a new coordinate (x_3, y_3) .
What are the conditions of the segment addition postulate?
The first states that an arbitrary point B should lie on the line segment AC only if all three points are collinear with each other. The second condition tells us that the distance AB and BC must be equal to the distance AC.
How to check whether the three points are collinear?
Using two methods, you can determine whether three arbitrary points are collinear. The first method uses the slope formula, while the second method uses the area of a triangle. Learn more about area with our Area tool.
How do you find the length of a segment using the segment addition postulate?
First, you need to measure the parts of the segments. After that, with the help of the formula for the segment addition postulate or by entering the segment data into our tool, you will get the desired results.
