Since the beginning of humankind, humankind has been interested in all kinds of geometrical shapes. Things like the Pythagorean theorem for right-angle triangles and the formula for the circle area are just proof that geometry is the most exciting area of math. One of those shapes is a trapezoid. A trapezoid is a “cousin” of shapes like rectangles and squares. For example, if you look at the rectangle from the proper perspective, you will see a trapezoid. Handbags, boats, and many packagings are all in a trapezoid shape. With our Trapezoid calculator you will be able to calculate area, angles and height of trapezoid.
In addition, if you are interested in math and geometry, you can find more useful tools on our site. Check out our Trigonometric Functions Calculator, Antilog Calculator, or some other in math section.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is a trapezoid – definition?
Trapezoid (sometimes called trapezium) is a polygon with four straight sides, two parallel. Parallel sides are bases, and the other two are called legs. That means that, by loose definition, a trapezoid is every quadrilateral with at least one pair of parallel sides. By this definition, shapes like rectangles and squares are trapezoids. However, an even stricter definition says that a trapezoid is a quadrilateral with exactly one pair of parallel sides.
Trapezoid perimeter and trapezoid angles
The formula for the perimeter of a trapezoid is like for any other polygon. It is just the sum of lengths of its sides. For isosceles trapezoid its even easier. Isosceles trapezoid is trapezoid which has equal legs. Now, if two straight lines are parallel, and one straight line intersects both, there is a relation between angles that line makes with two parallel lines.
For example, in the picture below, angles E and C and G and A are the same. Because angles B and H are the same, the sum of angles B and E is 180 degrees. That means that in trapezoid sum of two interior angles on the same leg is 180 degrees. The sum of all the angles in a trapezoid is 360 degrees. By knowing the look of our trapezoid, we could even use the sine and cosine functions to find these angles.
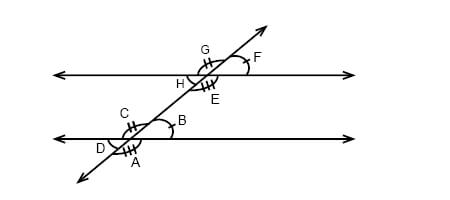
How to calculate the area of trapezoid?
There are a few ways to calculate the trapezoid area. The first is to divide the trapezoid into three shapes, one rectangle and two right-angle triangles. Then you can use our Area Calculator. This way seems easy since it’s not hard to calculate the area of those shapes, but the problem is that we need to know almost all parameters about our trapezoid to do it. So the more efficient way is to use the formula:
A=\frac{1}{2} \cdot (b_{1}+b_{2}) \cdot hWhere b1 and b2 are the lengths of trapezoid bases, and h is the shortest distance between our bases (more on that later).
On the other hand, we have a special calculator for calculating the area of a trapezoid, and to learn more about it.
Trapezoid properties
We can describe trapezium with more than just lengths of its edges. Other properties include perimeter, which is the sum of all of its sides, and area, which is a quantitative measure of interior space bounded by the edges of a trapezoid. There is also the median. Median is just an average of both trapezium bases. The formula for calculating the median is:
m=\frac{1}{2} \cdot (b_{1}+b_{2})And we can rewrite the formula above for calculating the area of the trapezoid as:
A=m \cdot h
Another property is the height of the trapezoid, which is the shortest distance between two bases. The main property of the height is that it forms right angles with both base b1 and base b2. Consequently, we have a right triangle formed on both sides of trapezoid.
How to find the height of a trapezoid?
The trapezoid height is the length of the line that goes from one base to another and is perpendicular to both bases. If we have area and both bases, we can calculate the height using the formula:
h=\frac{A}{m}Where m is the median of our trapezoid, however, we don’t have the area given in most cases, so we have to find another way.
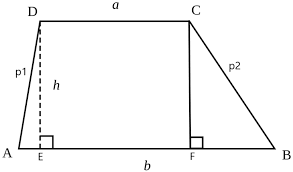
Let’s notice two triangles in the picture above. Those are triangle AED and triangle FBC. Notice that both of them are right-angle triangles (right angle formed with base b). Now we can use simple trigonometry and the Pythagorean theorem to find the height. If we know the area of one of these triangles, we can see the height given the one other side. From the diagram above, if we know the length of FB and area of triangle AFBC, for example, that is:
h=\frac{2\cdot A_{FBC}}{FB}If we know the angles on the bases and some of the sides of our trapezoid, we can use sine or cosine functions to find the height. In the picture above, if we know AD and angle EAD, we can use:
\sin(EAD)=\frac{h}{AD}h=\sin(EAD) \times AD
How to use our calculator?
When you choose the trapezoid calculator in our app, the app will present you a trapezoid picture, where everything is labelled. That is so we know which property we are changing when we enter values into numerical fields.
Our calculator has three sections. In the first one, you can enter the values of the bases and then enter the height (or area) to calculate the area (or height).
You can enter the legs (the other two sides) in the second one and calculate the perimeter. If you click on the Advanced Mode below, you can even see the median length (average of both bases).
If you entered all of those in the third section, you would see all angles in your trapezoid according to the picture.
For example, enter this data in the appropriate fields:
a(base)=8 \;cm\newline b(base)=4\;cm\newline h(height)=3\;cm\newline c=4\;cm\newline d=5\;cm
You should see the following:
Area(A)=18\;cm^{2}\newline
Median=6\;cm\newline
Perimeter(P)=21\;cm\newline
\alpha=48.59 \degree\newline
\beta=131.41\degreeOur calculator can even handle the other units of measure like inches and radians.
FAQ
Is trapezoid a parallelogram?
In geometry, a parallelogram is a quadrilateral with two pairs of parallel sides. A trapezoid is a quadrilateral with one pair of parallel sides. Given that every parallelogram by this definition has pair of parallel sides, that technically means that all parallelograms are trapezoids. The opposite only applies if the trapezoid has two pairs of parallel sides.
Is trapezoid a quadrilateral?
Quadrilateral is polygon with four sides and four angles. Trapezoid has four straight sides and four angles. That means that trapezoid is a quadrilateral.
How many sides does the trapezoid have?
A trapezoid is a quadrilateral, which means it has four straight sides. Other quadrilaterals include shapes like squares, rectangles, parallelograms, and rhombus.
Is rectangle a trapezoid?
It depends on how you define trapezoid. A loose definition of the trapezoid is that the trapezoid is quadrilateral with at least one pair of parallel sides. By this definition, every rectangle is a trapezoid. A more strict definition says that a trapezoid is a quadrilateral with one pair of parallel edges. By this definition, the rectangle is not a trapezoid.
Is square a trapezoid?
It depends on how you define trapezoid. A loose definition of a trapezoid is that a trapezoid is quadrilateral with at least one pair of parallel sides. By this definition, every square is a trapezoid. However, a more strict definition says that a trapezoid is a quadrilateral with exactly one pair of parallel edges. By this definition, a square is not a trapezoid.
