Trigonometric functions can be very difficult and time-consuming to understand and solve. In general, we have six main trig identities and for each both sum and difference formulas. Therefore, in total, we have 12 complex formulas that you need to remember in trigonometry.
Thankfully, this has been fixed by the introduction of our Sum and Difference Identities Calculator, which instantly helps us in solving sum and difference identities. If you want to check it out and learn what is an identity and how to use the calculator, feel free to skim through the text below.
For more trigonometry and math-related product, we’ve prepared for you a list of recommended ones below:
- Trigonometry Calculator
- Trigonometric Functions Calculator
- Law of Sines Calculator
- Law of Cosines Calculator
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
Trigonometric Functions
Undoubtedly trigonometry is a broad topic, and for us to understand trigonometric functions, we should first go back to ancient Greece, where it all began.
At that time, ancient mathematicians were interested in geometry, and they wanted to study the triangle in depth. Their fascination for the triangle led them to discover the famous Pythagorean theorem. This discovery was of crucial importance for trigonometric functions, as well.
The world of geometry is fairly chaotic, and there are rules we need to follow. Trigonometry builds on that same observation.
Trig functions describe the ratios between the sides of a right triangle. The picture below lists the formulas of all six trigonometric functions. We will cover more details in the next sections.
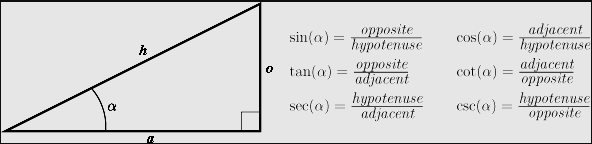
Domain and Range of Trigonometric Functions
The value of θ (theta) is the domain of the trigonometric functions, while the resultant value represents the range of the trig function. The domain values are shown in degrees or radians and the domain of the trigonometric function is a real number, but in some cases, the results may be infinite values. However, the trig function is a periodic function, by the definition.
| Trig functions | Domain | Range |
| Sin θ | (-∞, + ∞) | [-1, +1] |
| Cos θ | (-∞ +∞) | [-1, +1] |
| Tan θ | R – (2n + 1)π/2 | (-∞, +∞) |
| Cot θ | R – nπ | (-∞, +∞) |
| Sec θ | R – (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Cosec θ | R – nπ | (-∞, -1] U [+1, +∞) |
Note: We never do the calculation manually, because it’s not an easy task. In most cases, we use external tools such as calculators that we have built individually for each trig function. Feel free to look at the list below if you need to use them for calculations:
- Sine Calculator
- Cosine Calculator
- Tangent Calculator
- Cotangent Calculator
- Secant Calculator
- Cosecant Calculator
Sum and Difference Identities
The trigonometric identity have had real-world applications for centuries, including their use in calculating long distances.
Mainly, we use the sum and difference identities of sine, cosine, and tangent functions, but we have a few more trig identities. Their applications are different including finding the distance of the Earth from the Sun or measuring the height of a mountain.
We use sum and difference identities to solve various math problems and prove the trigonometric formulas and identities. In total, we have six main sum and difference formulas for the trigonometric functions:
{sin(A + B) = sinA cosB + cosA sinB}{sin(A - B) = sinA cosB - cosA sinB}{cos(A + B) = cosA cosB - sinA sinB}{cos(A - B) = cosA cosB + sinA sinB}tan(A + B) = \frac{(tanA + tanB)}{(1 - tanA \times tanB)}tan(A - B) = \frac{(tanA - tanB)}{(1 + tanA \times tanB)}Sine Addition and Cos Addition Formulas
The sum and difference formulas calculate the values of trigonometric functions by putting them in terms of fairly equal functions, but with different arguments. Essentially, we take the initial angle and decompose it into a sum or difference of two other angles. As a result, we find the initial value by using the new ones instead applying the sum or difference formula.
Let’s start and cover the two most used trigonometric formulas:
Sin addition formula:
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
Cos addition formula:
cos(α + β) = cos(α)cos(β) - sin(α)sin(β)
In case when the α angle and β angle are equal (α = β), the cos and sin addition formulas look like this:
sin(α + α) = sin(α)cos(α) + cos(α)sin(α)
cos(α + α) = cos(α)cos(α) - sin(α)sin(α)
Or in simpler terms:
sin(2α) = 2sin(α)cos(α)
cos(2α) = cos²(α) - sin²(α)
But, what about their difference identities? Well, since we already know that addition and subtraction are two almost the same operation, just with inverted signs, we can easily make the sin and cos difference identities using the formulas above:
Sine difference formula:
sin(α - β) = sin(α)cos(β) - cos(α)sin(β)
Cos difference formula:
cos(α - β) = cos(α)cos(β) + sin(α)sin(β)
Other Sum and Difference Trigonometric Identities
We’ve mentioned earlier that besides the main sine and cosine formulas, we also have more complicated trig identity, such as:
- tangent
- cotangent
- secant and
- cosecant
We can quickly and easily solve sine and cosine formulas, but it gets tricky and messy when we need to solve the tangent and cotangent sum and difference trig identities. Surely, one of the reasons why they can get complex is the fact that we need to solve fractions. What about secant and cosecant formulas? Well, that’s even worse and messier.
Here is the list of addition and difference formulas for tangent, cotangent, secant, and cosecant:
tan(x−y) = \frac{tan(x) – tan(y)}{1+tan(x) \times tan(y)}tan(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)}cot(x+y) = \frac{tan(x) + tan(y)}{1−tan(x) \times tan(y)}cot(x-y) = \frac{tan(x) - tan(y)}{1+tan(x) \times tan(y)}sec(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)}sec(x-y) = \frac{tan(x) - tan(y)}{1+tan(x) \times tan(y)}csc(x+y) = \frac{tan(x) + tan(y)}{1-tan(x) \times tan(y)}csc(x-y) = \frac{tan(x) - tan(y)}{1+tan(x) \times tan(y)}Sum and Difference Identities Calculator – How to Use?
I guess it was enough of theory. Now, it’s time to show you how you can quickly solve addition and difference identities for any of the 6 available options that you can choose from. Most importantly, you don’t have to calculate anything by yourself. Instead, utilize our Sum and Difference Identities Calculator and instantly get the result.
Steps:
- Choose one of the six given options from the dropdown list (sine, cosine, tangent, cotangent, secant, or cosecant)
- Enter α angle and β angle in degrees or radians
- Boom, you got the results!
Sum and Difference Identities Calculator – Example
Since we’ve explained how our calculator works, let’s put it into practice now and see how it goes in a real scenario.
Scenario: Let’s assume we want to solve the cosine and tangent trig identities for the angle α = 65° and the angle β = 20°.
Step #1:
- Choose the cosine function from the list
- Enter the α angle and the β angle in the respective fields
- See the result
cos(65° - 20°) = cos(65°) \times cos(20°) + sin(65°) \times sin(20°) = 0.423 \times 0.94 + 0.906 \times 0.342 = √2/2 = 0.707
Step #2:
- Choose the tangent function from the list
- Enter the angles in the respective angles fields
- See the result
FAQ
What are the trigonometric identities?
Trigonometric functions describe the ratios between a right triangle’s sides. By the definition, there are six basic trigonometric functions: sine function, cosine function, secant function, co-secant function, tangent function, and co-tangent function.
How to use sum and difference identities?
Essentially, we take the initial angle and decompose it into a sum or difference of two other angles. As a result, we find the initial value by using the new ones instead, applying the sum or difference formula.
What are the six sum trigonometric formulas?
There are six trigonometric identities. Each of them have both addition and difference formulas. Therefore, in total, we have 12 sum and difference formulas:
– sin(A + B) = sinA cosB + cosA sinB
– cos(A + B) = cosA cosB – sinA sinB
– tan(x+y) = (tan x + tan y) / (1− tan x tan y)
– cot(x+y) = (tan x + tan y) / (1− tan x tan y)
– sec(x+y) = (tan x + tan y) / (1− tan x tan y)
– csc(x+y) = (tan x + tan y) / (1− tan x tan y)
How do you find the sine sum and difference of two angles (35° and 93°)?
In order to solve the sine addition and difference of the two mentioned angles, we need to use the sine trigonometric formulas:
sin(A + B) = sinA cosB + cosA sinB = sin(35°) \times cos(93°) + cos(35°) \times sin(93°) = 0.574 \times -0.052 + 0.819 \times 0.999 = 0.788 sin(A - B) = sin(35°) \times cos(93°) - cos(35°) \times sin(93°) = 0.574 \times - 0.052 - 0.819 \times 0.999 = -0.848