Pentagon Calculator is used for calculating every aspect of a pentagon. For example, you can quickly find its area, perimeter, incircle radius, circumcircle radius, height and diagonal. Forget about boring formulas, do not bother yourselves with that. Let our calculator solve it for you in a second.
Check out math category if you need more math-related calculators besides this calculator.
What is a pentagon? How many sides does it have?
Pentagon is a geometric figure, polygon, with five sides and five angles. If at least one of them is not straight, we no longer say that it is a pentagon. We need to have five straight connected lines to form it, and they should not overlap.

Pentagon has two types of angles: interior and exterior. If we add each exterior angle to the sum, we realize that every pentagon has 540 degrees as the sum of exterior angles. On the contrary, interior angles are smaller, 72 degrees each, making it 360 degrees in a total of every pentagon. Similarly, there is another very similar geometric figure with six sides, called a hexagon.
It is derived from the Greek language, penta = five and gon = angle. Importantly, people started to use this geometric shape for multi-purposes long ago. The shape of a house or a ball resembles a lot like a pentagon. Apart from his, take a look at a diamond or a tent. Clearly, you will figure out that they naturally have their shape but are more polished and rounded.
Types of pentagons
Classification of pentagons is made upon certain factors: vertices, side length, and interior angles.
Thus, depending on those factors, we have four different types of pentagons:
Regular
If a pentagon is equilateral and every interior angle is equal, we call it a regular pentagon.
Irregular
An irregular pentagon is a pentagon of different sides and interior angles.
Convex
When a pentagon has all the interior angles less than 180 degrees with vertices pointing outwards, it is called a convex pentagon.
Concave
If we have a pentagon with an interior angle greater than 180 degrees and vertices pointing inwards, we call it a concave pentagon in geometry.
Area and perimeter of a regular pentagon
It’s important to understand that we have a different formula for calculating the area and perimeter of a regular pentagon compared to the formula we use for irregular. It’s mainly because the regular and irregular do not have the same properties.
How to calculate the area of a regular pentagon?
There are two ways to find the area of a pentagon, thus I will mention both of them.
The first way is if only its side is known, and we have no additional information. In this case, we use the formula:
Area = a^{2} \times \sqrt{(25 + 10 \sqrt{5})}\div 4
a – side length (square)
The second way is used if we don’t know the side length, but circumscribed circle radius is known. Then we make use of the formula:
Area = 5 \times R^{2} \times \sqrt{[(5 + \sqrt{5}) \div 2]} \div 4
R – circumscribed circle radius (square)
How to calculate perimeter of a regular pentagon?
Since a regular pentagon is equilateral, we can easily find its perimeter by multiplying the side length with the number of vertices – 5.
We calculate perimeter of a regular pentagon using this formula:
Perimeter = 5 \times a
a – number of vertices of a polygon
We use this same approach for calculating the perimeter of a hexagon and a square, as well.
Height and diagonal of a regular pentagon
If we connect each vertice with its opposite vertices, we will slice a pentagon by the intersecting lines (diagonals) into smaller parts, called pentagrams (they look like a small triangle). Thus, we find out that every regular pentagon has five diagonals.
Diagonal of pentagon formula
Diagonal = a \times (1 + \sqrt{5}) \div 2
a – side length
On the other side, let’s see how we can find the height of a regular pentagon. By its default definition, the height of a pentagon or any polygon is the distance between one pentagon’s side and the opposite vertex.
Height of pentagon formula
Height = a \times \sqrt{(5 + 2\sqrt{5})} \div 2
a – side length
We see that you only need to know the side length for calculating the height or diagonal of a pentagon.
Perimeter of pentagon formula
We already mentioned and gave the formula for calculating perimeter of a regular pentagon. In contrast, calculating the perimeter of irregular pentagons is a bit different (nothing scary).
Irregular pentagons have no equal sides, which means that our previous formula does not apply to them. Why? Because it is solely based on the condition that all five of them are equal. Therefore, the question arises, “how do we approach irregular pentagons and compute their perimeters?”.
We calculate it by adding all five side lengths of the particular pentagon, and the sum represents its perimeter.
Example:
We have a pentagon of side lengths: 3cm, 6cm, 2cm, 4cm, 5cm:
Perimeter = 3 + 6 + 2 +4 + 5 = 20 cm
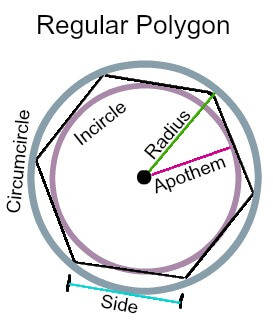
Radius (apothem) of pentagon formula
Radius (incircle), often called apothem, is a line drawn from the centre of a pentagon towards the medium point of one of its sides. We have the same number of apothems based on the number of sides. Since the pentagon has five of them, there are five apothems, then. It is important to mention that only regular pentagons have apothems.
There are two ways to find the incircle radius of a pentagon:
1) if we know the side length of the pentagon
r (apothem) = a \div 2 \times tan(x) \times 180 \div n
r – incircle radius
a – side length
n – number of sides (5 for pentagon)
2) if we know the circumcircle radius
r (apothem) = r \times cos(x) \times 180 \div n
r – incircle radius
n – number of sides (5 for pentagon)
Circumcircle radius of pentagon formula
Circumcircle radius is the distance between the centre of a pentagon and any of its vertices.
Same as for incircle radius, we can find it using two formulas:
1) if we know the length of one of its sides
R (Circumcircle radius) = a \div 2 \times sin(x) \times (180 \div n)
a – the side length
n – number of sides (5)
2) if we know the incircle radius
R (Circumcircle radius) = r \div cos(x) \times (180 \div n)
r – incircle radius
n – number of sides (5)
How to solve a regular pentagon using this pentagon calculator?
Now, we have a pretty solid knowledge about a pentagon and its parts, including all the formulas we need to know to calculate its parts. However, if you use those formulas, you need to apply them by yourself to calculate something. Happy news! Our Pentagon Calculator will handle that for you.
Pentagon Calculator can calculate all parts of the pentagon based on your input:
- side length (a)
- perimeter (P)
- area (A)
- diagonal (d)
- height (h)
- circumcircle radius (R)
- incircle radius (apothem)
Note: We can only use the Pentagon Calculator for regular pentagons, those equilateral.
Let’s go through an example to show you how the calculator works.

Take a look at the image above. What do you see? A building, right, massive building? Yes, but you can see that it has a pentagon shape, more specifically, a regular pentagon (equilateral).
Let’s imagine each side of the building is 20 meters, so what now? How do we calculate the radius, diagonals, area, and all these things?
We enter this value (20m) in the calculator for the field “Side (a)”, and the calculator will automatically calculate everything else.
Side (a) = 20 m
Perimeter (P) = 100 m
Area (A) = 688.19 m squared
Diagonal (d) = 32.36 m
Height (h) = 30.78 m
Circumcircle radius (R) = 17.01 m
Incircle radius (apothem) = 13.7638 m
