Probability of 3 Events Calculator

Use this Probability of 3 Events Calculator to calculate the following probabilities: 

• at least one event out of three occurring (union of three events); 
• intersection of three events (all three happening); 
• one event happening;
• of none of the occurring;

There’s a probability that only one of them will happen and a probability that none of them will happen. Learn about probability rules and its use in everyday life. Also, you can check 30 60 90 triangle and Cofunction Calculator, 45 45 90 triangle calculator, PSI to GPM Calculator, Trigonometry Calculator, gpm calculator.

Probability Calculator for 3 Events

This probability calculator may be used for three separate, random events. First, change the units to decimal value and enter the probability (possible chance) of each event as a percentage. The calculator will output the following once you’ve completed the three fields:

• at least one of the following three events is likely to occur:

P(A ∪ B ∪ C)

• the chances of all three occurrences occurring are as follows:

P(A ∩ B ∩ C)

• the probability of one of three occurrences occurring precisely once:

P(A ∩ B’ ∩ C’) + P(A’ ∩ B ∩ C’) + P(A’ ∩ B’ ∩ C)

• probability of none of the events happening:

P(∅)

You may also enter two numbers in the first and second portions of this calculator. Depending on the values you provide. Keep in mind that each probability must be a value between 0 and 1 (or in percentage values as 0% and 100%, respectively). If you choose, you may modify the unit to a decimal values.

Probability of 3 events formula

The probability of three events occurring can be calculated using the formula:

P(A and B and C) = P(A) x P(B|A) x P(C|A and B)

where P(A) is the probability of event A occurring, P(B|A) is the probability of event B occurring given that event A has occurred, and P(C|A and B) is the probability of event C occurring given that both event A and event B have occurred.

This formula is known as the multiplication rule of probability and can be extended to any number of events. The general formula for the probability of n events occurring is:

P(A1 and A2 and … and An) = P(A1) x P(A2|A1) x P(A3|A1 and A2) x … x P(An|A1 and A2 and … and An-1)

In words, this formula states that the probability of n events occurring is equal to the probability of the first event multiplied by the probability of the second event given that the first event has occurred, multiplied by the probability of the third event given that both the first and second events have occurred, and so on, up to the probability of the nth event given that all previous events have occurred.

This formula can be used to calculate the probability of complex events that depend on multiple factors. For example, if we want to calculate the probability of getting a red card, a number card, and a face card in a standard deck of cards, we can use the multiplication rule of probability to calculate:

P(red and number and face) = P(red) x P(number|red) x P(face|red and number)

where P(red) is the probability of drawing a red card, P(number|red) is the probability of drawing a number card given that we have already drawn a red card, and P(face|red and number) is the probability of drawing a face card given that we have already drawn a red card and a number card. By multiplying these probabilities, we can find the probability of getting all three events.

What are the rules of probability?

The enumeration of various occurrences becomes more complex as the number of variables in a frequency distribution rises. Therefore, some fundamental guidelines will be beneficial instead of continuing to portray every circumstance as a multidimensional sample or sample space.

The following are the Four Probability Rules

1. Addition Rule applies if one event is the result of the union of two other occurrences. For example, if A and B are both events, then the following rule applies.

P(A or B) = P(A) + P(B) − P(A and B)

2. Complementary Rule applies whenever one occurrence is the counterpart of another. In particular, if A is an event, the following rule applies.

P(not A) =1 − P(A)

3. Conditional Rule will apply whenever just partial information about an occurrence is available. For example, if event A is already known to have happened and the probability of event B is sought, the following rule applies.

P(B, given A) = P(A and B)P(A)P(B, given A) = P(A and B) / P(A)

4. Finally, the Multiplication Rule will apply anytime an event occurs at the intersection of two additional events. That is, events A and B must occur at the same time. As a result, if A and B are events, the following rule applies.

P(A and B) = P(A) x P(B, given A)

Probability rules for 3 events & how to calculate the probability of 3 independent events?

Assume a fair die was rolled, and you’re asked to estimate the probability that it was a five. Your answer is chance of 1/6 because there are six equally likely outcomes. Assume, however, that you are provided with the additional information that the number rolled was odd value before you make your answer.

Then, because there are only three odd numbers that may be rolled, one of which is a five, you’d alter your estimate of the probability of a five being rolled from 1/6 to 1/3.

The conditional probability of A given B, represented as P(AB), is the updated probability that an event A has occurred. Taking into account the extra knowledge that another event B has certainly occurred on this trial of the experiment. The computational formula in the following definition may be derived from the logic used in this example.

Although we usually anticipate the conditional probability P(AB) to differ from the probability P(A) of A, this is not always the case. When P(AB) = P(A), the presence of B has no bearing on the probability of A. The occurrence of event A is unrelated to the occurrence of event B.

It can be demonstrated using algebra that the equality P(AB) = P(A) exists if and only if the equality P(AB) = P(A)P(B) exists, which is true if and only if P(BA) = P(B). The following definition is based on this.

A and B are unrelated occurrences (i.e., events whose probability of occurring together is the product of their individual probabilities). 

P(A∩B) = P(A) x P(B)

Probability of mutually exclusive events

The probability of two occurrences colliding may be computed using the addition rule when they are mutually exclusive. For example, we know that rolling a number larger than four and a number less than three are mutually exclusive events with nothing in common when rolling a die.

To calculate the probability of this occurring, just multiply the probability of rolling a number more than four by the probability of rolling a number less than three. The following are the symbols, with the capital P denoting “probability of”:

P(greater than four or less than three) = P(greater than four) + P(less than three) = 2/6 + 2/6 = 4/6.

If the occurrences are not mutually exclusive, we must remove the probability of the events intersecting. For example, given random events A and B, we remove the probability of the intersection to account for the risk of double-counting those items that appear in both A and B.

P(A U B) = P(A) + P(B) – P(A ∩ B).

How to calculate the probability of multiple events?

The probability of many events is a fascinating issue in statistics and mathematics. When we’re watching several occurrences and want specific outcomes, chance or possibility of each one, understanding how to compute, the probability of multiple events comes in helpful.

When two or more vents occur, the probability of numerous events lets us determine our chances of attaining the desired results. Whether the presented occurrences are independent or dependent will significantly impact the assessed probability.

When we try to compute the probability of seeing two or more events, we get the probability of multiple events. Experiments in which we see many actions at the same time, drawing cards with various conditions, or guessing the outcome of a multi-colored spinning are examples.

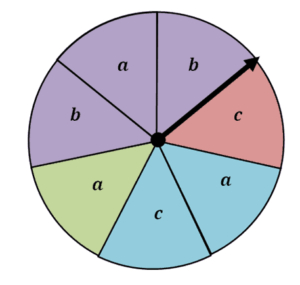
We can observe that the spinner is divided into seven sections. Each of which is identifiable by its own color or label.

Here are some instances of several occurrences that the spinners can reveal:

• Calculating the chances of spinning a violet or an.
• calculating the chances of spinning a blue or a

We must compute the probability of two occurrences occurring at the same time under these two circumstances. The probability of multiple events measures the possibility of two or more events occurring at the same time. We occasionally search for the probability of one or two events occurring and if these outcomes overlap.

FAQ

Tags

• featured