45 45 90 Triangle Calculator – Right Triangle

Today, calculators make many things easier, no more hours of torture to check that the calculation is correct. All we need is to enter everything for the calculation into the calculator, and it gives us the correct answer. If you need hypotenuse calculation, measurement, and ratio, make it easy for yourself and easily determine all this coupled with our calculator.

In case you are looking for more calculators in math, physics, finance, health and other visit our official page. Besides this 45 45 90 triangle, make sure to see our related 30 60 90 triangle and trigonometry calculator as well.

Take a look other related calculators, such as:

• Phase shift calculator
• Power reducing formula calculator
• Probability calculator 3 events
• Cofunction calculator
• Sum and difference identities calculator
• Segment addition postulate calculator
• Fundamental counting principle calculator
• Condensing logarithms calculator
• Population density calculator

What is a 45 45 90 triangle?

45 45 90  triangle is an isosceles triangle that has two equal sides. Since the third side is not equal to the others, it is called the hypotenuse. Equal pages are called legs. In a right triangle, the hypotenuse is larger than each leg; the sides are also two triangle heights.

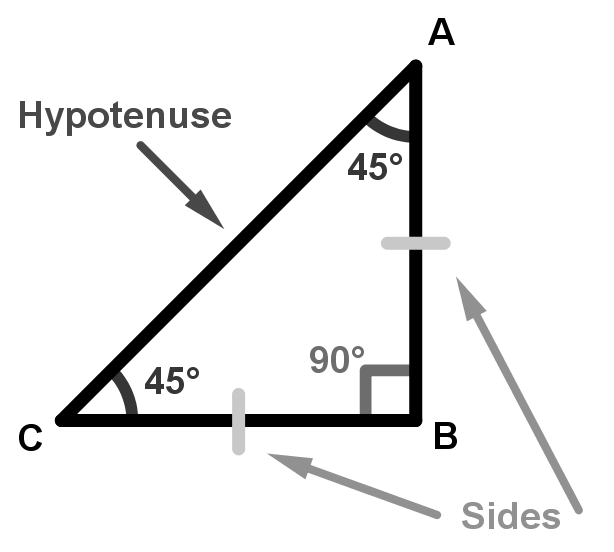
How to solve a 45 45 90 triangle? Formula

Using Pythagoras’ theorem and six trigonometric functions, you can use our calculator to solve a right triangle. Since a right triangle has one angle of 90 degrees, and calculating a right triangle requires measuring only one of the two acute angles. 

We can use Pythagorean Theorem and calculator to calculate the hypotenuse:

c^2=a^2+b^2 \newline c^2=1^2+1^2   \newline c^2=1+1 \newline c^2=\sqrt{2}

With the hypotenuse we have the necessary information to determine the following:

sin 45° = \frac{1}{\sqrt{2}}

cos 45° = \frac{1}{\sqrt{2}}

tan 45° = \frac{1}{1} = 1

So we concluded that the sinus is \frac{1}{\sqrt{2}} since 1 is the lenght of the opposite side of 45° and the hypotenuse is \sqrt{2}

For cosine, we need an adjacent hypotenuse which gives us \frac{1}{\sqrt{2}}

And the last, for the tangent, which is the opposite of the adjacent, we have \frac{1}{1} , or simply put, just 1.

How to solve a 45 45 90 triangle: an example

Calculate the value of the leg in a right triangle if the length of one leg is 3 cm and the hypotenuse is 5 cm.

Here’s an opportunity to make it easier for ourselves with our calculator.

The longest side of a right triangle is the hypotenuse and is denoted by the letter c. The other two sides are called legs and are denoted by a and b, and they are joined at right angles. It doesn’t matter which page we mark with a and b. It is important not to confuse them with the c.

a = 3c

c = 5cm

We use Pythagoras’ theorem to determine any side of a right triangle. When using a calculator, we must have the values of the other two pages. Therefore, if we know two pages, calculators will easily help us find the third unknown value.

b = ?

c² = a² + b²

5² = 3² + b²

In solving the equation, it is necessary to calculate the squares of the values we know and transfer them to one side while leaving the square of the page we are looking for on the other side.

5² = 3² + b²

25 = 9 + b²

b² = 25 – 9

b² = 16

To solve these equations, we can make it easier for ourselves by using a calculator, and we use the basics of algebra. To get rid of the square, it is necessary to remove the square root of both sides. Since we are looking for the value of the length, it must be positive to ignore the negative values of the square roots.

b² = 16

b = 4

The value of leg b is 4cm.

45 45 90 triangle ratio

Recall that the triangle of a special rectangle 45 45 90 is an isosceles triangle with two equal sides and one larger side. Simply put, the ratio of the lengths of the sides of a triangle with a special rectangle of 45 45 90 must be 1 : 1 : \sqrt{2}

45 45 90 triangle rules and properties

• The angles of this triangle are in proportion 1 : 1 : 2
• Their sum is 180° that is \alpha = \beta = 45° = \frac{\pi }{4} i \gamma = 90° = \frac{\pi }{2}
• The aspect ratio is 1 : 1 : \sqrt{2}
• The only possible triangle with this direction in Euclidean geometry is an isosceles right triangle, and in hyperbolic geometry there are infinitely many.
• Of all the triangles, this one has the lowest hypotenuse-leg ratio \frac{\sqrt{2}}{2}

45 45 90 triangle sides

There is a special connection between the measures of the sides of 45 45 90 angles.

45 45 90 triangle whose pages have proportion 1 : 1 : \sqrt{2}

The measures of the sides are \chi , \chi and \sqrt[\chi ]{2}

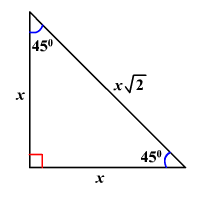
In a 45 45 90 triangle, the hypotenuse lenght is \sqrt{2} times the length of a leg.

45 45 90 triangle area

In a 45-45-90 triangle, the two legs are congruent and the hypotenuse is sqrt(2) times the length of either leg.

Let’s say that each leg of the triangle has a length of “a”. Then, using the Pythagorean theorem, we can find the length of the hypotenuse:

c^2 = a^2 + a^2 c^2 = 2a^2 c = a*sqrt(2)

So the area of the triangle can be found by:

A = (1/2) * base * height

where the base and height are the two legs of the triangle. Since they are congruent, we can use either one as the base and the other as the height. Let’s use “a” as the base. Then:

A = (1/2) * a * a A = a^2/2

So, the area of the 45-45-90 triangle with legs of length “a” is equal to a squared divided by 2 or A = a^2/2.

Solve the Hypotenuse, Leg, Area, Perimeter

Every triangle with one angle equal to 90° is called a right angled triangle

The area A of a right triangle with sides a and b is given by

A = ( 1 / 2 ) a b

The perimeter P of a right triangle with sides a and b and hypotenuse h is given by

P = a + b + h

Using the Pythagorean theorem, we can write

h² = a² + b²

which gives

h = \sqrt{} (a² + b²)

Hence the perimeter can be written in terms of a and b only as follows:

P = a + b + \sqrt{} (a² + b²)

Example:

Find the area and perimeter of a right angled triangle with sides of lengths 0.4 ft and 0.3 ft. (Try using a calculator)

Let side a = 0.4, b = 0.3 and h being the hypotenuse.

Area = (1 / 2) a b = (1 / 2) 0.4 × 0.3 = 0.06 ft²

Perimeter = a + b + h = a + b + \sqrt{} (a² + b²) = 0.4 + 0.3 + \sqrt{} ( 0.4² + 0.3²) = 1.2 ft

FAQ