Our circle calculator enables you to calculate radius (r), diameter (d), circumference (c) and area (A) of a circle. It is one of our most simple calculators in terms of usage. This calculator can be helpful whether you are studying math in elementary school, high school or college. If any of this interests you, you can check out the essay we wrote, teaching you how to calculate and understand all of this yourself.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
Circle definition
A circle is a round-shaped figure without any corners or edges. It is also defined as a round plane figure whose boundary consists of points from a given distance from a fixed point (the center). It is one of the most basic shapes you know from everyday life. A circle is just a line, and people usually confuse it with a disc (a disc includes the circle together with its interior). The first people that observed and measured the circle were ancient Egyptian mathematicians and engineers. Suppose you want a more precise and mathematically correct circle definition. It is a special kind of eclipse in which the two focuses are coincident, the eccentricity equals 0, and the semi-major and the semi-minor axes are equal.
Special lines of the circle
Circles’ most essential lines are chord, secant, tangent, and most importantly, radius and diameter. We will not define the first three, not because they are unnecessary, but because the second two help us calculate all we need. Instead, we will describe them and give you a more detailed explanation later in the text.
Radius and Diameter definition
A line segment whose endpoints are points on a circle and center is defined as a radius. The name radius comes from Latin radius, which means ray and a chariot wheel. Radius formulas will be presented later in this text.
Diameter is any straight line segment that goes through the center of a circle and whose endpoints lie on the circle. It is also the most extended chord of the circle. The same thing goes with the diameter, and its formulas will be presented later in the text.
Circle properties
Circle has many properties and rules. We will not name each of them, but we will present to you all the types of circle properties. There are 5 of them, and each one of them represents a different area, point or a line. And if you want more detail on them, you can find it all on “Circle – Wikipedia”. Its properties are chord, tangent, theorems, inscribed angles and sagitta.
Unit circle
In math, a unit circle is a circle that has a radius of 1. It is effortless and often used to learn and talk about angles and lengths. Considering that the radius is 1, we can directly measure cosine, sine and tangent. Another thing specific about a unit circle is that its center is (0,0). It is an exciting and easy way to explain circle math to someone.
Circle formulas
When doing circle math, you will have to deal with many formulas. However, in the end, most of them are simple. Therefore, we will not show them to you yet. Nevertheless, below this, we wrote four separate paragraphs on calculating the properties of a circle. Another important thing about calculating anything relating to the circle is knowing about the pi (π). We will teach you about it together with all the other formulas. However, in the end, the easiest way not to bother with all those facts is to use our simple calculator. You can download the calculator at “CalCon Calculator – Apps on Google Play” or use the online version.
What is pi (π)?
The number π (spelt out as “pi”) is used in math as a constant. It equals approximately 3.14159. It was first defined in Euclidean geometry as the ratio of a circle’s circumference to its diameter. More precisely, pi is an irrational number that can be approximated as a fraction.
\frac{22}{7}This number’s decimal presentation never settles nor ends into a repeating pattern.
How to find the area of a circle?
The area of a circle is the space occupied by the circle’s boundary. Circle area is marked as “A” in math. This is because calculating the area can be very important in further calculations. There are a few ways to calculate it, but this is the most used one.
A=\pi r^{2}How to find the radius of a circle?
As we already defined, a circle radius is any line segment from its perimeter to its center in geometry. In modern usage, it is also called the length of a circle. The radius of a circle can be calculated through the circumference, the area and the diameter. Calculating it is very important because you will probably be using it in many other formulas or equations. As you can see, those are three straightforward formulas.
r=\frac{C}{2\pi } r=\sqrt{\frac{A}{\pi }}r=\frac{d}{2}Make sure to check out this related Radius of a Sphere Calculator.
How to find the center of a circle?
The easiest way to say it is that the center of a circle is the point equidistant from the points on edge. There is no formula to finding a circles center. However, if you are interested in finding some circles center, there are a few excellent ways to do it that you can look up online.
How to find the circumference of a circle?
The circumference of a circle can also be named the perimeter of the circle. In other words, the circumference would be the length of a circle as if it were straightened out to a line segment. It is elementary to calculate, and here are two ways to do it.
C=\pi d
C=2\pi r
How to find the diameter of a circle?
The diameter of a circle is a line from one side of a circle directly to the opposite side through the center. It is also the most extended chord of a circle. So there are three different ways to find it, and here they are.
d=2r
d=\frac{C}{\pi }d=2\sqrt{\frac{A}{\pi }}Chord of a circle
The chord of a circle is a line segment that links two locations on the circle’s circumference. That being said, we can say that the diameter is the most extended chord. There are two ways to calculate the length of a chord, and here they are.
Chord\; Lenght=2\sqrt{(r^{2}-d^{2})}In the second formula you will have to apply trigonometry.
Chord\; Lenght=2rsin(\frac{c}{2})In this case “c” does not represent the circumference but the angle.
Concentric circles
Concentric circles can be defined as all the circles that share the same center. Also, for two circles to be concentric, they must have different radiuses.
Squaring the circle
At some point in your life you probably wondered if it was possible to turn a circle into a square. Squaring the circle is a problem that ancient geometers proposed. The challenge is constructing a square with the same area as a given circle in a few steps. It was being researched for centuries and in 1882. the task was proven to be impossible. The expression “squaring the circle” became a famous metaphor for doing the impossible.
Circle and 3D shapes – sphere, cylinder and cone
Sphere, cylinder and cone are D3 objects with a circle in some area of them. They are one of the most basic and commonly used geometric shapes, so we wrote a few words about them
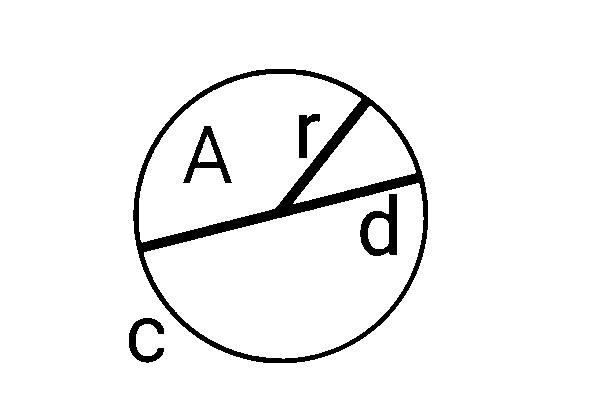
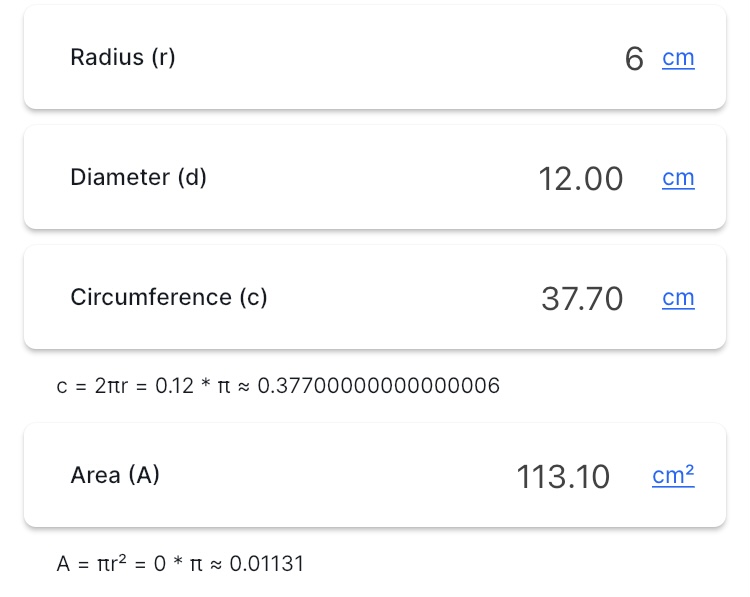
How to use this calculator?
As it is presented in the picture above, it is one of the most straightforward calculators to use. You can calculate everything by knowing just one fact about the circle. In this example, we typed in just the radius and instantly got all the answers. You don’t have to know anything about these equations or formulas, our calculator does the job for you. Many calculators on the internet just make it harder for you, but our one can calculate everything using the most simple formula.
