Hexagon Calculator

The hexagon form is one of nature’s most popular shapes, with applications ranging from honeycomb patterns to hexagon tiles for mirrors. Not only will we explain why the 6-sided polygon is so popular, but we’ll also show you how to draw hexagon sides correctly. In addition, you may learn how to utilize our hexagon calculator to simplify any study concerning this 6-sided form and explore various geometrical features and computations, such as how to estimate the area of a hexagon.

Take a look other related calculators, such as:

• Phase shift calculator
• 30 60 90 triangle calculator
• 45 45 90 triangle calculator
• Power reducing formula calculator
• Probability calculator 3 events
• Cofunction calculator
• Sum and difference identities calculator
• Trigonometry calculator
• Segment addition postulate calculator
• Fundamental counting principle calculator
• Condensing logarithms calculator
• Population density calculator
• Area conversion calculator

How many sides does a hexagon have?

A hexagon is a two-dimensional geometric polygon with six sides and angles. It doesn’t have any curved sides, and all of the lines are straight. A normal hexagon’s interior angles total 720 degrees.

It’s useful to know which form of hexagon we’re looking at when asking, “how many sides does a hexagon have?” Each hexagon contains six sides, each with its own set of characteristics. Hexagons come in four distinct shapes. Regular hexagons, irregular hexagons, concave hexagons, and convex hexagons are the four types of hexagons. A regular hexagon must possess three characteristics:

• the hexagon’s sides must all be the same length.
• Each of the inner angles must be 120 degrees.
• When all of the inside angles are added together, the total must be 720 degrees.

We divide a hexagon may into six equilateral triangles. These will all be the same size and maybe reassembled in a honeycomb pattern. Tessellation is what happens when we do this with a bunch of hexagons.

Hexagon definition, what is a hexagon?

A hexagon is a two-dimensional geometric shape with six sides. A hexagon’s sides are all straight, not bent. Honeycombs made by bees to store honey, pollen, and larvae have hexagons. We find them in Ireland’s Giant’s Causeway, which comprises interconnecting volcanic rock columns. While these are the most well-known examples, hexagons may also be found in many other places in nature, including the bond shapes of specific molecules, crystal formations, turtle shell patterns, and more.

But why hexagons in particular? What makes them so unique? It’s all a matter of efficiency, really. When you make a hexagon grid, the shapes completely interlock, and there are no gaps. However, as compared to other forms that interlock in this way, each hexagon’s lines are as short as they may be. Longer lines will be seen in any other interlocking form. As a result, they use less resources in their construction and have high compressive strength.

Area of hexagon

The area of a hexagon is the area that exists between the hexagon’s sides. A hexagon is a two-dimensional form with nine diagonals and 720 degrees of internal angles. Estimation of the area of a hexagon is using a variety of techniques and we represent it in square units such as m2, cm2, in2, or ft2.

Hexagon area formula: how to find the area of a hexagon

We’ll now look at various methods for calculating the area of a hexagon. The simplest method is to utilize our hexagon calculator, which has a built-in area conversion function. No matter how many sides a polygon has, as long as it is a regular polygon, the method for calculating its area remains the same:

area = apothem x perimeter / 2

The apothem is the distance between either side’s midway and the center to refresh your memory. You may think of it as the height of an equilateral triangle made up of one hexagonal side and two radii (each of the colored areas in the image above). However, because a perpendicular line defines the Euclidean distance, the apothem may alternatively be thought of as the distance between the center and any side of the hexagon.

All sides of the regular triangle are the same length, which is the length of the hexagonal side they make. This will be referred to as a. In this situation, the height of a triangle is h = 3/2 x a, which is the precise value of the apothem. We’d like to remind you that it stands for square root. We may begin with the maths using this:

A₀ = a x h / 2

= a x √3/2 x a / 2

= √3/4 x a²

Where A0 denotes the area of each of the equilateral triangles into which the hexagon has been partitioned. We derive the hexagon area formula by multiplying this area by six (since we have six triangles):

A = 6 x A₀ = 6 x √3/4 x a²

A = 3 x √3/2 x a²

= (√3/2 x a) x (6 x a) /2

= apothem x perimeter /2

Diagonals of a hexagon

The hexagon has a total of nine diagonals, three of which are lengthy diagonals that cross the center point, while the other six comprise the hexagon’s so-called “height.” Because the nine diagonals create six equilateral triangles, and the radius matches the side length, determining the length of each diagonal line is simple.

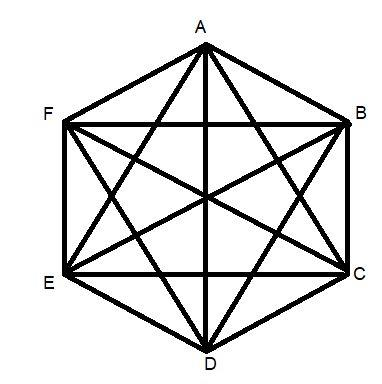
Our hexagon calculator may also save you time by calculating the diagonal lengths of the hexagon. The two types of diagonals are calculated as follows:

Long diagonals – They always cross the hexagon’s central point. The length of such a diagonal is equal to two edge lengths, as shown in the diagram above:

2 * a = D

Short diagonals – do not pass through the center. They’re made by connecting two vertices while leaving precisely one between them. Their total length is

d = 3 * a.

Hexagon angles

Internal angles are all set at 120 degrees. The dihedral group D6 is made up of six rotational symmetries (rotational symmetry of order six) and six reflection symmetries (six lines of symmetry) in a regular hexagon. A regular hexagon’s longest diagonals, which link diametrically opposing vertices, are double the length of one side. This shows that an equilateral triangle has a vertex in the regular hexagon’s center and shares one side with the hexagon and that the regular hexagon may be partitioned into six equilateral triangles.

Multiply 180(n – 2) to get the internal angle, where “n” is the number of sides (in this example, six). To find the answer, multiply 180 by 4. Next, subtract the number of angles, which is six in this case. This gives you the angle measurement in degrees, which should be 120.

Divide 360 by “n,” where “n” is the number of angles to get outside or outside the hexagon. You should obtain 60 degrees in this situation.

How to draw a hexagon?

Draw a perfect hexagon with a ruler and a protractor. Next, use a circular shape and a ruler to guide your hand for a rougher hexagon. Finally, if perfection isn’t important, you can draw a basic hexagon using just a pencil and your imagination.

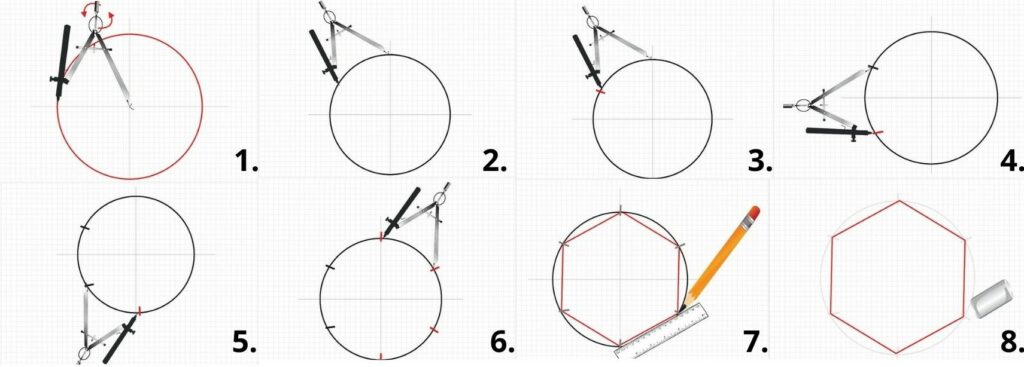
Steps in drawing a hexagon

Step 1: Using a compass, draw a circle. In your compass, stick a pencil. Adjust the compass’s width to match the radius of your circle. It might be as little as a few inches or millimeters in width.

Step 2: Bring the compass point to the circle’s edge. Bring it up to the top of the circle. Change the compass’s angle or settings at your own risk.

Step 3: Make a tiny mark on the circle’s edge using the pencil. You’ll be wiping it afterward, so make it distinct but not too black. Remember to keep the compass at the same angle you set it.

Step 4: Move the compass point to the spot where you created the mark. Place the point exactly where the mark is.

Step 5: Make another mark on the circle’s edge using a pencil. This should result in a second mark that is spaced apart from the first. Continue to go around the circle in either a clockwise or counterclockwise direction.

Step 6. Using the same approach, make the final four markings. You should eventually return to the point where you began. If you don’t, the angle of your compass may alter as you worked, either due to over-squeezing or letting it slack a little.

Step 7: Using a ruler, connect the dots. The six points of your hexagon are the spots where your markings intersect the circle’s edge. Next, draw a straight line segment connecting the neighboring dots with your ruler and pencil.

Step 8: Remove the guiding lines from your drawing. Your initial circle, the markings around the edges, and any extra marks you made along the way are all included. Your ideal hexagon should be complete once you’ve deleted your guidelines.

Circumradius and inradius

The circumradius and inradius are another essential set of numbers in a hexagon. The circumradius is the regular hexagon’s circumference radius that contains all of its vertices. The radius of the largest circle totally enclosed within the hexagon is the inradius.

Circumradius: To calculate the radius of a circle circumscribed on a regular hexagon, measure the distance between the hexagon’s central point (the circle’s center) and any vertices. R = a is the simple formula.

Inradius: The radius of a circle encircled by a regular hexagon is half its height, which is also the apothem: r = 3/2 x a.

The easiest way to find a hexagon side area

The hexagon calculator lets you determine the number of useful characteristics for the 6-sided form we call a hexagon. This calculator is as easy to use as it gets, requiring only one of the parameters to compute all of the others and including a built-in length conversion tool for each.

We’ve gone over all of the calculator’s settings, but for clarity and completeness, we’ll go through them again now:

• Area – a two-dimensional surface encircled by a hexagonal form;
• Side Length – is the distance between one vertex and the next.
• We call the sum of the lengths of all hexagon sides the perimeter.
• Long Diagonal – is the distance between one vertex and the opposing vertex.
• Short Diagonal – The distance between two vertices that are separated by another vertex.
• The circumcircle radius – is the distance from the center to a vertex (the same as the hexagon’s radius), while the incircle radius is the same as the apothem.

Hexagon tiles and real-world uses of the 6-sided polygon

Hexagons are one of the most commonly utilized polygons in the world, and everyone enjoys a good real-life application. Starting with human applications, hexagon tiles for floors are the simplest (and possibly least intriguing). A hexagon is a great form since it fits together neatly to cover any needed space.

The next example is universal to all polygons, but it’s still worth looking at. The opening of the sensor in photography is usually always polygonal. The aperture is an element of the camera that controls many of the attributes and aspects of the images it produces. Due to the diffraction grating effect, the form of highly brilliant (point-like) objects is the most surprising.

Astronomy is one of the most significant uses of hexagons in the contemporary age, and it’s closely connected to the one we discussed in photography. Their light has less energy when it reaches the Earth due to relativistic effects (equivalent to time dilation and length contraction). The redshift is the name for this phenomenon.

As a result, we obtain a small quantity of energy with a longer wavelength than we want. The easiest method to overcome this is to construct as large a telescope as feasible. The challenge is that manufacturing a one-piece lens or mirror bigger than a few meters is nearly unfeasible, not to mention logistical problems.

Due to the geometrical principles of a “Cassegrain telescope,” making such a large mirror enhances the telescope’s angular resolution as well as the magnification factor. As a result, we may argue that regular hexagons allow us to see better, further, and more clearly than we could with single-piece lenses or mirrors.

Honeycomb pattern – why the 6-sided shape is so prevalent in nature?

We can group regular hexagons side by side in the honeycomb design. There are no gaps between them since they totally cover the whole surface they span. This honeycomb pattern may be seen not just in honeycombs (surprise! ) but also in a variety of other natural settings. It is so common that it may be considered the default form when opposing forces are at work and spheres aren’t attainable, owing to the nature of the situation.

Regular hexagons are the most prevalent polygonal form seen in nature, ranging from bee colonies to rock fractures to chemical chemistry (even in the building blocks of life: proteins). And there’s a good explanation for it: hexagonal angles. When we line up hexagons side by side, the 120 degrees angle is the most mechanically stable of them all, and it’s also the angle at which the sides meet at the vertices.

The way 120 degrees angles distribute forces (and hence stress) along two hexagon sides makes it a mechanically efficient and stable design. Hexagons offer a substantial benefit in this regard. Regular hexagons also have the ability to completely fill a surface with no gaps between them (along with regular triangles and squares). Furthermore, among these surface-filling polygons, the regular 6-sided form has the shortest perimeter for the most area, making it particularly efficient.

Also, a bubble made with water, soap, and part of your own breath always takes on a spherical form. Bubbles are a fun way to visualize the advantages of hexagons over other forms. However, there are a few sites in nature where regular hexagonal patterns may be found:

• Honeycombs
• Compounds of organic origin
• Bubbles stacked on top of one other
• Formations of rock (such as Giant’s)
• Insects’ eyes

FAQ