As a particular part of math science, you can apply geometry in everyday situations. So this way, we can mention the case of flying a kite. You must have found yourself in a position of looking high into the sky following the trajectory of a kite. And, at the same time, wondering how you could calculate the area of a kite. Just for you and other curious people, we present you CalCon calculator that measures the area of a kite. You can read more about the measurement method below.
What Is the Area of a Kite?
We will begin with an explanation of the geometric body of a kite. According to Euclidean math and geometry, kites are quadrangular shapes whose sides you can group into two pairs of equal lengths that stand next to each other. They are also known as deltoid bodies. The word “deltoid” refers to a deltoid curve that is an unrelated geometric object.
When it comes to the kite area, it is presented as the space that surrounds the kite. The parts that make up the kite are four corners, four sides, and two diagonals. Based on these elements, you can determine the formula for calculating the tendon area, which we will explain below. It is also important to mention that you can view the area as covered with the kite. Since this shape resembles an elongated square or rhombus, the kite also does not equal all sides.
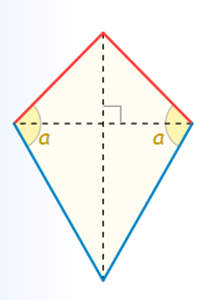
Area of kite formula
You have decided to make the kite yourself, and the surface will represent the size of the material used to make it. If you take pieces of wood, they will convey the kite’s diagonals that will support and tighten the fabric around the pieces of wood, forming the appearance of a kite. Given the above, the calculation formula looks like this:
A = \frac{p\cdot q}{2}where p and q are diagonals.
When it comes to calculating using our calculator, we distinguish two situations. Our calculator offers the ability to calculate the area of a kite if you know the values of both diagonals or the values of opposite sides and the angle they close.
If you know the diagonal values, then it is enough to enter the data in the predicted places marked with the letters e and f. The calculation formula looks like this:
A = \frac{e\cdot f}{2}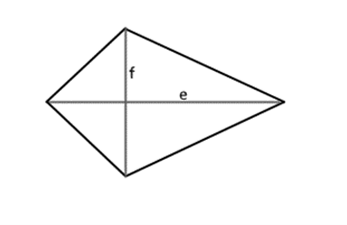
When you know the values of the lengths of two non-congruent pages, and the angles between those pages marked a and b, then you need to use the following formula:
A = a\cdot b\cdot sin\alpha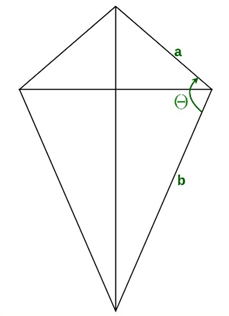
Kite perimeter
It is necessary to have the values of each pair of unequal sides a and b for calculating the perimeter of a kite. The sum of all the sides of a kite represents the perimeter of a kite. Therefore, the formula for calculating the perimeter has the following appearance:
Perimeter = a+b+a+b = 2\cdot (a+b)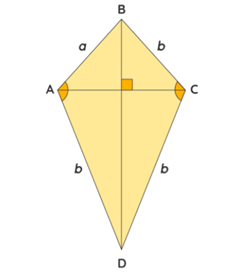
Kite Area & Perimeter – work with steps
Example 1:
We will give the first example to calculate the perimeter of a kite:
Side a of a kite has a length of 11 inches, while side b has a length of 17 inches.
It is necessary to find the perimeter of a kite.
In this example, the perimeter of a kite has a value of 56 inches.
Example 2:
We will consider the situation that you want to give your closest friend a chocolate bar in a box in a kite shape. You want to decorate the package to paste a photo of you and your friend on top. First, you must determine the area of the box cover if the diagonal values are in the following amounts of 10 inches and 15 inches, respectively.
You can use the formula:
A = \frac{e\cdot f}{2} = \frac{10\cdot 15}{2} = 75inch^{2}How to find the diagonals of a kite?
As a unique geometric shape, the kite contains two diagonals whose lengths are different. They intersect as such, making a right angle. In the following example, you will learn how to calculate the value of the diagonal length having the value of the area of a kite.
Example:
It is known that the value of the total area of a kite is 144inch2 and that the value of one diagonal is twice as long as the value of the other. Find the length of each diagonal.
Solution:
As you have previously become acquainted with the formula for calculating the area, with minor changes in the appearance of the formula, you can calculate the values of the diagonals. With the information given at the beginning that one diagonal is twice as long as the other, the formula has the following appearance:
A = \frac{a\cdot b}{2}a : b = 1 : 2
a = 2b
For ease of further calculation, we will assume that diagonal a denote by x and diagonal b by 2x.
144 = \frac{x\cdot 2x}{2} \Rightarrow 288 = 2\cdot x^{2} \Rightarrow x^{2} = 144 \Rightarrow x = 12inchAfter calculating the x, diagonal a has a value of 12 inches, while the value of diagonal b is 24 inches.
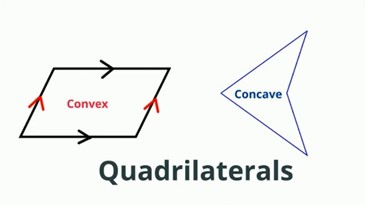
Convex and concave kites
Kites can most often be found in a convex shape, while less often in a concave one called a “dart” kite. Also, in math, you can find them as quadrilaterals. Convex types of kites are those whose internal angles have a value of fewer than 180 degrees. Otherwise, for concave shapes, at least one of the angles has a value greater than 180 degrees. With the procedure of measuring the area for these types of kites, the process is the same in the case of using our calculator and deciding to use the formula.
Properties of kites
Knowing the properties of this geometric shape can help you solve problems where you know the values of pages and angles. The properties include two consecutive sides, matching non-peak angles, and diagonals of different lengths. In addition to these properties, it is essential to note that you should be familiar with the properties of other related geometric bodies such as trapezoids, parallelograms, rhombuses, rectangles, and squares.
Is a kite a rhombus?
The main visible difference between a rhombus and a kite is that in a rhombus, all sides are equal, while in a kite, the situation is the existence of two adjacent equal sides. Therefore, we cannot say that a kite is a rhombus, but the opposite is true where every rhombus is a kite. While with a kite, depending on the shape, length of the pages, the values of the angles may or may not mean that each kite is a rhombus.
