Triangle Area Calculator

With our Triangle Area Calculator, you can calculate the area of any triangle you want. Since ancient times, geometry has been the area of math that interested many people. And there is a reason for that. From astronomy to architecture, we could describe various patterns mathematically, even in nature. We can describe any shape in two dimensions with its edges and area.

The area is the quantitative measure that expresses space bounded by a certain shape in math. So it is no surprise that this parameter is very important in real life. For calculating the area of other shapes, you can use many of our other calculators like Area of a Rectangle Calculator or Area of a Circle Calculator.

Take a look other related calculators, such as:

• Phase shift calculator
• 30 60 90 triangle calculator
• 45 45 90 triangle calculator
• Power reducing formula calculator
• Probability calculator 3 events
• Cofunction calculator
• Sum and difference identities calculator
• Trigonometry calculator
• Segment addition postulate calculator
• Fundamental counting principle calculator
• Condensing logarithms calculator
• Population density calculator

What is a triangle in geometry?

As children in math class, we all learned about the family of shapes like polygon and circle. Polygons are closed 2D shapes with straight edges. So rectangle is, and a circle isn’t a polygon. Usually, the name of such a polygon tells us how many sides that polygon has.

For example, there are pentagons, quadrilaterals, and so on. The important thing to note here is that polygon can’t have a number of edges smaller than three.

A polygon with three sides is called a triangle. There are all sorts of triangles. For example, an equilateral triangle is a triangle with all edges equal in length. The isosceles triangle has two sides equal.

How to solve the area of the triangle – rules?

When solving for the area of a triangle, you must know a few things. First of all, the area can’t be negative; such a shape doesn’t exist. When you think about it, it is obvious that there are just several measuring units in shape.

Secondly, we can’t find the area of some shapes without knowing some of the other parameters. In the case of triangles, there are a few we can calculate area depending on what info we know about the shape, like the lengths of its sides or angles.

Area of the triangle formula?

The formula to find the area of a triangle depends on the case. We can use the following formulas depending on the parameters we know.

Case 1 – When we know the base and the height of the triangle

A right-angle triangle is a triangle with one angle equal to 90 degrees. The longest side of the right angle triangle is its hypotenuse. The other two are called legs or catheti. We can calculate the area of the right angle triangle using the formula:

Area\space =\space \frac{a\cdot b}{2}

Where a and b are legs, but wait, you say. We are interested in calculating the area of any triangle, not just the right ones. And to do that, you need the height of a triangle.

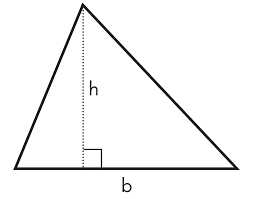
Height is the distance between a vertex (tip) of a triangle and the opposite side (base) of the shortest length. This definition is a little different with obtuse triangles, but we will stick with it now. We will notice that it divides the triangle into two right-angle triangles from the picture above. So if we write the area of our triangle as the sum of areas of those two triangles, in the end, we will get:

Area\space =\space\frac{h \cdot b}{2}

Given the height and the base of a triangle, we can get the areas of two simpler triangles. You could even use our Area of a Right Triangle Calculator or other calculators.

Case 2 -When we know three sides

Calculating the are of a triangle given three edges is done by using Heron’s formula. Derivation of this formula is a little more complex, so we won’t go into details. To find the area of the triangle with three sides, a, b, c, use the following formula:

Area\space =\space\sqrt{s\cdot (s-a) \cdot (s-b) \cdot (s-c)}

Where s is the half of the perimeter or:

s\space =\space\frac{a+b+c}{2}

Case 3 – When we know two angles and the side between them

In trigonometry, one of the basic laws is the Law of sines, and it says that the quotient of angles and the opposing sides is the same. In addition, we must notice that the sum of all the angles in the triangle is 180 degrees.

Using these two facts, we can find the rest of the sides and third angle given just two angles and side between them, and then we can use another method to solve for the area. Check out our Law of Sines Calculator, Law of Cosines Calculator and many other calculators used in trigonometry.

Case 4 – When we know two sides and the angle between them

When we know two edges a,b, and angle between them delta, the area of our triangle is given with the following:

Area\space=\space \frac{1}{2} \cdot a\cdot b\cdot \sin{\delta}

This kind of problem is the SAS triangle (we know side–angle–side).

Area of the equilateral triangle formula?

Triangle is equilateral if all of its sides are of the same length. If we apply the Pythagorean theorem on one half of this triangle, we get that height is equal to:

Height\space =\space \frac{\sqrt{3}\cdot a}{2}

where a is the side length. Then we can just plug in this value in our formula above to get:

Area\;of\;equilateral\;triangle\space =\space\frac{\sqrt{3}\cdot a^{2}}{4}

Triangle Area Calculator – How to use it?

When you open Triangle Area Calculator in our app, you will be greeted with a few things. The first field in this calculator is a field that you can use to pick the right option for calculating. These are all cases we talked about earlier.

Then, depending on what option you pick, the drawing will be displayed with labels that we are about to give labeled. For example, if you pick calculating with three sides in the first field, only three edges, a, b, and c, will be labeled.

Below, the app will present you with fields to enter your parameters. When you enter your values into the calculator, the last field result will appear. Note that, like with every other calculator in our app, you can choose units different from the default.

Triangle Area Calculator – Example?

Let’s get the area of the triangle with the following parameters:

a\space =\space 10cm\newline
b\space =\space 15cm\newline
c\space =\space 13cm

In our calculator, in the “Given” field, pick the “three sides (SSS)” option. Then in the next three fields, just enter the information above. In the Area field below, you will see the result:

Area\space =\space 64.0625cm^{2}

FAQ