The cotangent(cot(x)) calculator will enable you to calculate the cotangent of an angle that is not 90 degrees. It is essential in mathematics as one of the more complex trigonometric functions. With the help of this article and our calculator, you will grasp this abnormal function. We also have a step-by-step solution on our calculator and some examples here.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is cot(x)?
The cotangent of cot(x) is the cosine of x divided by the sine of x. Unlike sine and cosine that we calculate from the right triangle, we calculate cotangent from either tangent or if we have cosine and sine given.
It is important to note that cotangent is not the inverse function of cosine or tangent. Rather, cotangent has an inverse function written as arccot(x) (or inverse of a cotangent). The domain of inverse cotangent for x is [negative infinity, x, positive infinity]. Hence we can conclude, for y-axis domain is 0 < y < pi.
As previously stated, the cotangent of x is the cosine divided by the sine. If we look at the right angle, we can better understand such a matter. For example, in the following figure, we have a right triangle. First, we would calculate cosine, second sine. Finally, we would get cot(x) after dividing those two values.
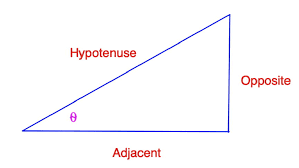
Cotangent formula
The Formula for the cotangent requires us to know either the tangent of both the sine and the cosine. For example, cotangent is equal to the reciprocal value of the tangent. At the same time, if we insert the value of deviation, the sine of x divided by the cosine of x, we get the Formula for cot(x). Let’s focus on the right triangle from figure 1. We know that the sine value is the ratio of the opposite side and the hypotenuse. Next, we calculate the cosine. The cosine from the previous figure is equivalent to the balance of the adjacent side and the hypotenuse.
Now we can define cotangent using the first option. If we insert the values of the sine and the cosine, we get the Formula.
Cotangent(x) = \frac{1}{Tangent(x)}Another way of calculating cotangent is by considering the common value of the tangent. We divide the sine and the cosine with cosine(x) to get the following Formula. Above the fraction line, we have cosine(x)/cosine(x), equal to one. Below the fraction line we have sine(x)/cosine(x).
If we insert the value of tangent. We get the formula for the cotangent using the tangent of x.
Cotangent graph
Unlike the sine or the cosine, the cotangent has different domains. For instance, the domain for cot(x) is [negative infinitive, positive infinity] on the y-axis. The domain of the x-axis is [0, pi]. First, let’s look at the graph of the cot(x).
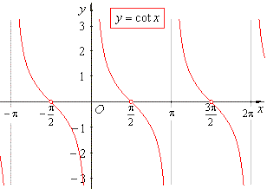
For instance, we can conclude that the period of the cotangent is pi, where pi is a constant equal to 3,14. As we stated before, cotangent has none when it comes to amplitude. The domain of y ranges from negative infinity to positive infinity. That means that graph goes on forever to infinity. Another crucial fact is derived when we glance over the figure for the tangent and the cotangent graphs. For instance, we have the charts of both the tangent and the cotangent in the following figure.
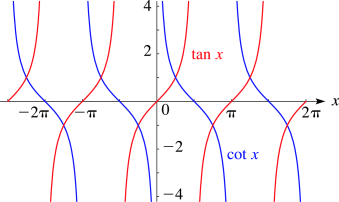
We can notice that the graphs for our two functions face different directions. However, we can also note the intersection of the two functions. They intersect for values of negative one and positive. Both of these functions have the same domain on the y-axis. However, The range is different. The cotangent has a range of 0 to pi. Tangent has a range of -pi/2 to pi/2.
Cotangent unit circle
We have already talked about unit circles in our sine, cosine, and similar trigonometric function calculators. However, the unit circle for the cotangent and the tangent are not the same. For instance, the unit circle for the cosine uses specific points on a circle to determine the value of the most common angles. So, on the contrary, we cannot use the same unit circle for the tangent and cotangent that we use for the cosine and the sine. For this example, let’s look at two unit circles. The first unit circle is the cosines & the sines. The other one is the cotangent unit circle.
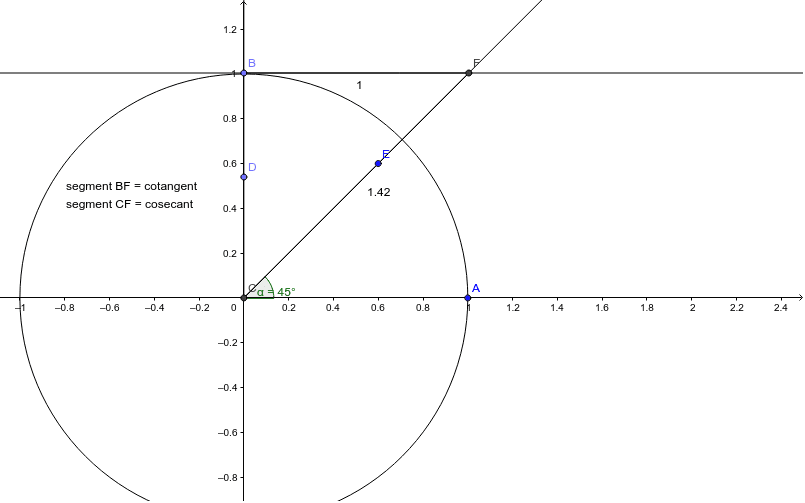
As you can see, our unit circle has a line parallel to the x-axis and is a tangent to our unit circle. The names tangent and cotangent got their names from this case. They are both tangent to the unit circle. The difference is how they tangent unit circle at pi/2 and 0. In addition, tangent tangents unit circle at 0(or 2pi).
We have the tangent and the cotangent unit circle in the following figure.
Notice that the cotangent is tangent to the unit circle at pi/2. How do we use a unit circle? If we are giving a certain angle. For example, the angle x = pi/4. Now let’s go back to our unit circle. On it, for the angle of pi/4, on the tangent line, we have the value of one.
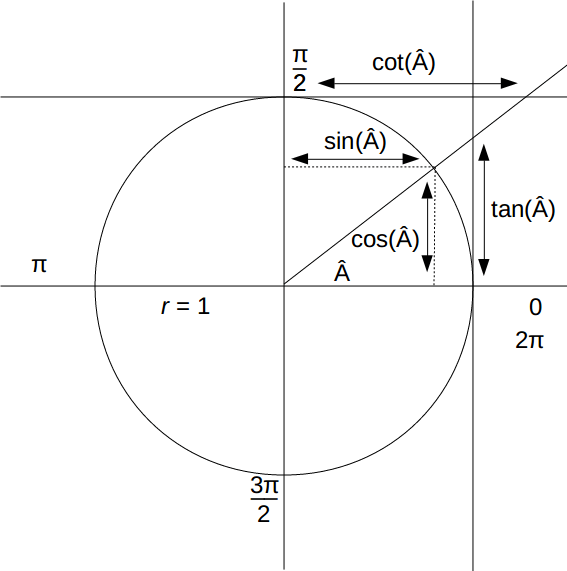
How to calculate the cotangent of a given angle?
When calculating the cotangent of an angle, we have a lot of tools we can use. The first option is to use the unit circle. Then, if we get a task to calculate the cotangent of an angle, we can use the last figure to calculate the cotangent’s most common values.
Problem: Calculate the cotangent & tangent of x = pi/3. Looking at the unit circle, we can see that for the angle of pi/3, the cotangent value is the root of 3 over 3. Using our tangent unit circle, we can define the tangent value for the angle of x = pi/3. Tan(pi/3) = root of 3
Using the tangent Formula is another way to calculate the cotangent of a given angle. Let’s write the procedure first.
Cotangent(x) = \frac{1}{Tangent(x)}Now we can solve the problem using multiple ways. For example, if we have only the sides of a triangle, we could use the sines and the cosines to calculate cotangent. We can also use tangents. We know that cotangent is the reciprocal value of tangent. So the Formula would be.
Cotangent(x) = \frac{cosine(x)}{sine(x)}Problem: Calculate the cot(x) of the angle x. The sides of the right triangle are: the opposite of the angle x is 20cm, the adjacent to the angle x is 30 cm. First of all, we must calculate the hypotenuse. The hypotenuse formula.
Hypotenuse = \sqrt{(adjacent\;side)^2 + (opposite\;side)^2}Hypotenuse = 36cm. Next, we calculate the sine and the cosine of this angle. We can use the sine and the cosine formula. If you are unsure how to calculate the sine and the cosine, please check our other calculators for further explanation. After calculating the sine( 33,7 degrees) and the cosine(33,5 degrees), we can determine the value of cot(x). We are using the Formula.
Cotangent = \frac{cosine(x)}{sine(x)}We get that the cot(x) equals to about 44.7 degrees( cot of 45 degrees equals one). Another useful calculator is the angle conversion calculator that you can use when converting degrees to radians.
Applications of the cotangent function
Cotangent, and trigonometry, are used in a lot of subjects. Some of the topics where trigonometry is crucial include aviation, criminology, marine biology, navigation, calculating the height of buildings, etc.
In aviation and navigation, trigonometry calculates the distance traveled, distance to the goal, and many other important facts. Today the trigonometric functions are most notably used in architecture(to calculate the heights of buildings). Usually, they are calculators, as working manually can be tedious. Another use of these functions is in video games. For example, a popular game, “Super Mario”, uses a 2D space where the character moves by the x-axis and y-axis. Using the previously stated formulas, you could calculate the jump distance Mario makes. Finally, in criminology, we use trigonometric functions to approximate where, for example, the shooter stood.
Related trigonometric functions
When it comes to related trigonometric functions most notable one is tangent. This is because tangent represents the expected value of cotangent. However, it is crucial to note that processes such as the sine or the cosine also are related. To show this connection between the two functions, we must first consider what tangent is equal to is. Tangent(x) = sine(x)/cosine(x). Then, if we insert this formula into the first-mentioned formula, we can get the cotangent value by its sines and cosines. Cotangent(x) = cosine(x)/sine(x).
Example: using the cotangent calculator
To use our “Calcon” cotangent calculator, first, download our app from the google play store or Apple app store. Next, in the search bar, enter “Cotangent calculator”. Once the app finds the appropriate calculator, you will use it. First, enter the value of the angle you wish to find the cotangent for. After pressing calculate, it will display the results and the step-by-step guide on calculating manually.
