This Trigonometric Functions Calculator can quickly determine the values of six trig functions. Not only will you find the three fundamental functions – sine, cosine, and tangent – but also their reciprocals: cosecant, secant, and cotangent. Scroll down to discover more about trigonometric ratios, where to obtain sin cos tan charts, and how to recall function definitions using the mnemonic rule. Also, there is our Law of Cosines and Law of Sines posts to help you with cosine and sine theorems.
Our 45 45 90 triangle calculator will also help you with your trigonometry tasks.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Sum and difference identities calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
- Perimeter Calculator
What are trigonometric functions?
For trigonometry, a broader understanding of angle is necessary than for geometry. The solid circular arc in the illustration represents an angle A with a vertex at V and starting and terminal sides of VP and VQ, respectively. This angle is created by rotating a line segment counterclockwise around the point V from the location VP to the position VQ.
The clockwise rotation of the line segment from point VP to position VQ produces a second angle A′ with the identical beginning and terminal sides. Angles formed by counterclockwise rotations are positive, whereas those generated by clockwise rotations are negative. Less than one full rotation of the line segment around the point V produces the positive angle A and the negative angle A′ in the figure. The line segment is rotated one or more full rotations before coming to rest at VQ to produce all additional positive and negative angles with the identical beginning and terminal sides.
To establish trigonometric functions for any angle A, set it on a rectangular coordinate system with the vertex at the origin and the beginning side along the positive x-axis; r (positive) is the distance from V to any point Q on the terminal side of A; and (x, y) are the rectangular coordinates of Q. A trigonometric function has the same value for all coterminal angles, as is obvious. When n is an integer, sin (A 360n) = sin A; the other five functions have similar relationships. The trigonometric functions are periodic, with a period of 360° or 180°, as a result of these findings.
Sine, cosine, tangent and other trig functions: cosecant, secant and cotangent. Trigonometric ratios
The trigonometric functions of an angle are sine, cosine, and tangent. These trig functions can be defined in the context of a right triangle if the angle is sharp. Starting with the terminology for triangle sides, we may call the sides of a right triangle
- hypotenuse – you’ve undoubtedly heard that phrase before when studying about the Pythagorean theorem. So it’s the right triangle’s longest side – the one opposite the right angle (90°).
- adjacent side – the side that is not a hypotenuse and forms the angle of interest (in our example, angle ). Both the angle of interest and the correct angle are on this side.
- opposite side of the angle of interest (in this example, angle alpha) is called the opposing side.
- The reciprocal of the sine is the cosecant. The hypotenuse to the opposite is the ratio. Cosecant is abbreviated as csc, for example csc (30°), and its range is csc (alpha) >= 1 to csc (alpha) <= -1.
- The reciprocal of the cosine is secant. The ratio of the hypotenuse to the adjacent is the hypotenuse-to-adjacent ratio. Secant is abbreviated as sec, for example sec (30°), and its range is sec (alpha) >= 1 to sec (alpha)<= -1.
- The reciprocal of the tangent is the cotangent. It’s the proportion of one side to the other. Cotangent is abbreviated as cot, for example, cot (30°), and its range is from negative infinity < cot (alpha) < positive infinity
Trigonometric functions formulas
The sine function of an angle is the ratio of the length of an opposing side to the length of the hypotenuse. The worth of sin should be:
Sina= Opposite / Hypotenuse=CB / CA.
The ratio of the length of the neighbouring side to the length of the hypotenuse is the cos function formula. The cos function may be calculated using this formula:
Cosa = Adjacent / Hypotenuse = AB / CA.
The tan function formula is the length of the opposing side of a right-angled triangle divided by the length of the adjacent side. The learner should be aware that the tan function may be represented as a ratio of sine and cos. As a result, the tan function will be written as:
Tana = Opposite / Adjacent = CB / BA or
Tana = sina / cosa.
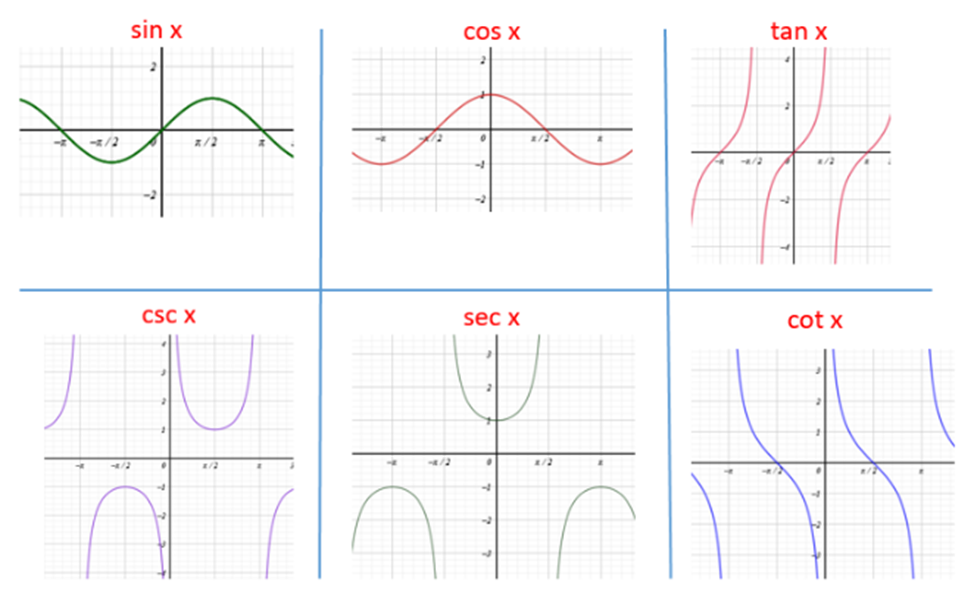
Charts of sin cos tan csc sec cot
The graphs of the trig functions sin, cos, tan, csc, sec, and cot are shown in the diagrams below. The three cofunction identities are useful because they can be used to transform any trig function into its function. Such as sine into cosine. Find the values of the original trig function before graphing reciprocal trigonometric functions. Then, plot the ordered pair on the coordinate plane using the reciprocal of each value.
The y = sin x, y = cos x, and y = tan x functions are used to graph the reciprocal trigonometric functions (y = csc x, y = sec x, and y = cot x).