Cosecant Calculator

Cosecant Calculator sounds amazing! Even if you’ve taken a trigonometry course, you could have missed this one because we don’t utilize it very often. Nonetheless, in math, the CSC is a well-defined function that may still be found in textbooks. As a result, we’ve put up this amazing tool and essay to address the question, “What is CSC?” We’ll also show you the cosecant formula and graph to go along with it.

What is cosecant? The cosecant formula

So, what exactly is a cosecant? The hypotenuse is split by the side (or leg) on the opposite side of the angle. In fact, even if we scale the triangle to double its original size, the values of the functions (including CSC x) will not change. There is. However, a cost to be paid. There is a technique to transfer the entire logic to any real integer, including a negative one, as the angle. Switching from triangles to two-dimensional Euclidean space, i.e. the plane is the key.

Let A = (x,y) be a plane point, and indicate by the angle that runs counterclockwise from the positive half of the horizontal axis to the line segment between 0 and A. Obviously, the angle can be more than 90 degrees. Even better, it can travel beyond a complete 360-degree angle! In such a situation, we simply consider the 360 a complete lap around (0,0), and we begin the second one. We can now have negative angles because we’ve defined it to be directed. So we just reverse the direction, going clockwise instead of counterclockwise, for them.

Now that we’ve covered all the angles, let’s decode the CSC meaning (and all the other functions, for that matter). The rule is straightforward: remember the notation for the point A = (x,y) and substitute a for y, b for x, and c for:

\sqrt{(x^2+y^2)}

So, with this new notation, what is the cosecant? First, we acquire the new CSC formula by following the preceding methods:

csc(x)=\frac{\sqrt{x^2+y^2}}{y}

Cosecant graph

Because the cosine and tangent graphs are among the most frequent trigonometric functions, it’s likely that you’ve encountered them before. However, CSC x is not, so you may have missed it. It’s a shame because it’s rather amusing to look at. Making a brief drawing of the sine function first is a very effective technique for charting the cosecant function (reciprocal). You may draw the asymptotes of the cosecant function through the x-intercepts (where the curve crosses the x-axis) of the sine function with the sine drawing in place. You may also use the sine function’s maximum and lowest values to find the cosecant function’s minimum and maximum points (also known as turning points).

• Draw the graph of y = sin x from –4 to 4, as depicted in diagram.

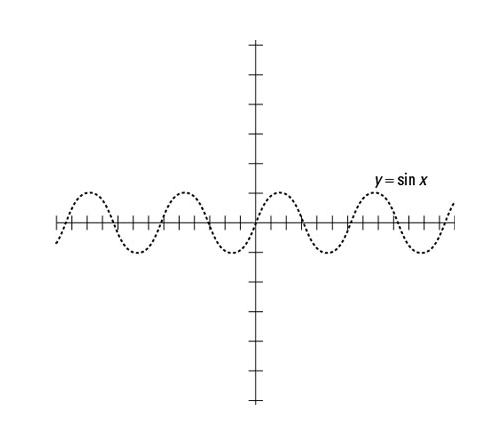
• As shown in the diagram, draw the vertical asymptotes via the x-intercepts.

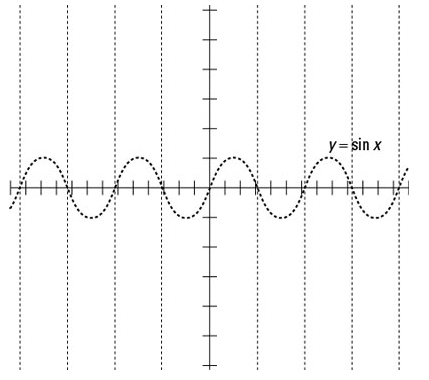
• As indicated in the diagram, draw y = CSC x between the asymptotes and down to (and up to) the sine curve.

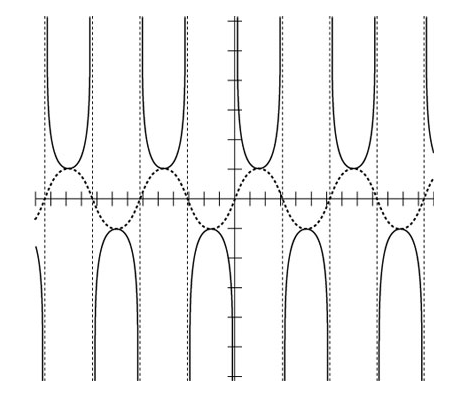
The cosecant is a function that runs from the top to the bottom of the sine curve. After sketching the cosecant curve with the asymptotes and reciprocal as guides, delete the unnecessary lines, leaving only y = CSC x. The following diagram depicts how this function appears on its own.

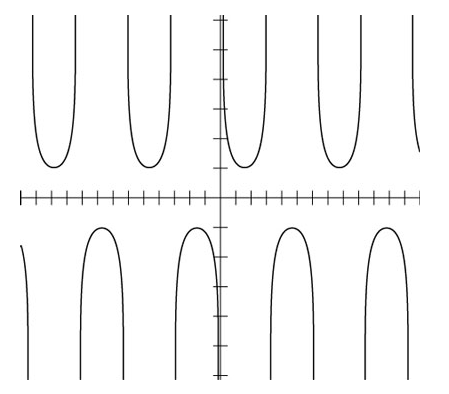
All values equal to or higher than 1 and all values equal to or less than –1 are included in the cosecant function’s range. In the diagram above, you can see that there is a function value gap between 1 and –1. Like all other trig functions, the cosecant curve has a pattern that repeats itself repeatedly.

How to find CSC: alternative CSC formulas?

The hypotenuse of a right triangle is divided by the side opposite the angle. Notice how we utilize the same lengths in the sine definition. The only difference is that they are inverted there. As a result, we get the following alternative cosecant formulas:

csc(x) = (sin(x))^{-1} or

csc(x) = \frac{1}{sin(x)}

However, it should be noted that this does not imply that CSC x is the inverse of sin x. That’s arcsin, which takes the value of the sine function and returns the angle that corresponds to it. The -1 in the exponent, on the other hand, simply says that CSC x is the inverse of sin x.

After that, we may extract another fascinating cosecant formula by taking this new CSC meaning and recalling a basic trigonometric identity for the cotangent.

\frac{cot(x)}{cos(x)} = \frac{cos(x)}{sin(x)} \cdot \frac{1}{cos(x)} = \frac{1}{sin(x)} = csc(x)

Function in trigonometry: CSC math

Trigonometric functions (also known as circular functions, angle functions, or goniometric functions) are real functions that connect the angle of a right-angled triangle to ratios of two side lengths in mathematics. They are widely employed in all geodetic studies, including navigation, solid mechanics, celestial mechanics, geodesy, and many more. They are among the simplest periodic functions, and as a result, they are frequently employed in Fourier analysis to examine periodic events.

The sine, cosine, and tangent are the most extensively utilized trigonometric functions in modern mathematics. The cosecant, secant, and cotangent are their reciprocals, which are less commonly employed. Each of these six trigonometric functions has an inverse function and a hyperbolic function analog.

Only acute angles are defined in the first definitions of trigonometric functions, which are connected to right-angle triangles. Geometrical definitions utilizing the conventional unit circle (i.e., a circle with radius 1 unit) are sometimes used to extend the sine and cosine functions to functions whose domain is the entire real line; then, the domain of the other functions is the real line with some isolated points removed. In modern definitions, trigonometric functions are expressed as infinite series or as differential equation solutions. This permits the domains of sine and cosine functions to be extended to the entire complex plane and the domains of other trigonometric functions to be extended to the complex plane with certain isolated points eliminated. 

Table of cosecant values

GRADES	RADIANS	COSECANT
0º	0	±∞
30º	π/6	2
45º	π/4	1,4144
60º	π/3	1,1547
90º	π/2	1
135º	3π/4	1,4144
180º	π	±∞
225º	5π/4	-1,4144
270º	3π/2	-1

FAQ