Cosine is one of the basic trigonometric functions. First, we will cover some basics about cosine and other related trigonometry functions. If you ever wondered what cosine, unit circle, and how to calculate cos(x), this Cosine Calculator is for you.

Meanwhile, find other interesting calculators on our sites, such as Pay Raise Calculator or something else from the finance category. Maybe you want to quit smoking. If so, check how much money you’ll save using our Quit Smoking Calculator.

What is cosine-cos(x)?

Cosine or cos or cos(x) is one of the trigonometric functions, together with sine, tangent, and cotangent. In math, cos is the ratio of the adjacent side and the hypotenuse. Most commonly, we face right-angle triangles. Right triangles (or right-angled triangles) have one angle of 90 degrees. Therefore, we need to understand its parts when calculating trigonometric functions in this triangle. For example, we have a figure that depicts a right triangle.

Right triangle cosine
Figure 1: Right-angle triangle

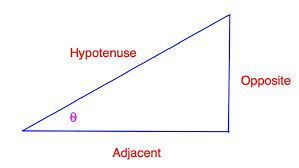
The hypotenuse is only possible in the right-angle triangles. It is the longest side of any right triangle. One characteristic of the hypotenuse is that it is the opposite of the 90-degree angle. The side that is the closest to the angle that we are calculating is called the adjacent side. It is important to note that the adjoining side cannot be the hypotenuse.

Like all trigonometric functions, cos(x) also has inverse functions. The inverse function of cos(x) is arccosine, arccos or arccos(x) or just inverse cosine. One important fact is that secant – sec(x) is not the inverse cosine function. To find the inverse of cos(x), we use a unit circle (more about unit circle later in the article). Cosine is defined as the dividend of the adjacent side and the hypotenuse.

Cosine formula

Looking at the last figure, we can write the cos formula as:

\cos(x) = \frac{Adjacent\;side}{Hypotenuse}

In some cases, we would need to calculate hypotenuse. For example, if we remember the procedure for the tangent, we can find cosine that way. 

\tan(x) = \frac{\sin(x)}{\cos(x)} => \cos(x) = \frac {\sin(x)}{\tan (x)}

The cosine formula enables us to calculate the cosine of the angle, but we can also calculate hypotenuse or adjacent sides if they are unknown.

Table of common cos(x) values

For a more straightforward calculation and solving tasks, mathematicians made a table of the most common trigonometric values. This table consists of five fundamental values in the first quadrant, and then those values are similar with a bit of twist.

The first value of 0 degrees corresponds to the negative value of pi = 3,141592 (or 180 degrees). However, the value of 45 degrees is exceptional. Both the sine and the cosine for the angle of 45 degrees have the same value. The same goes for the tangent and the cotangent for the angle of 45 degrees.

You might have noticed that we sometimes use degrees and sometimes use radians. If you are unsure of radians to degrees conversion, check out our Angle Conversion Calculator. 

When we glance over other values, we may conclude one more thing – the similarity of the values. For example, the cosine has the value of 1 at 0 radians (0 degrees) and the negative one at pi radians (180 degrees). On a unit circle or typical table, the angles of the first five angles are just nonpositive in the second quadrant. 

Cosine rules

Unlike the cosine formula we previously mentioned, we use the cosine rule on right triangles but also on any other triangle. Most trigonometric functions have these rules. To describe the cosine rule, let’s first look at the following figure.

Non-right-angle triangle
Figure 2: Non-right-angle triangle

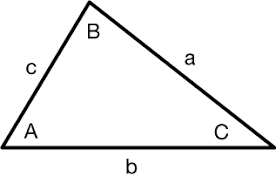
This triangle is not a right-angle triangle. So our cosine formula does not work here. No problem. Cosine rule comes to the rescue. As mentioned previously, we can use it on any triangle, so this one is not a problem even if it is not a right-angle triangle. Let’s write this rule as a formula.

c^2=a^2+b^2-2\cdot a\cdot b\cdot \cos(C)

With the cosine rule, we can calculate the angle of any triangle. However, we can also use the cosine rule to calculate the triangle sides. One disadvantage of this rule is that we must know either all sides (if we are calculating the angle) or two sides and the angle between them (if we calculate the remaining side).

Problem: Let’s say we have side a and side b, whose lengths are equal to 20 cm and 30 cm, respectfully. We have the angle between them, C = 30 degrees. Calculate the remaining side. If we use the previously mentioned cosine formula, we get the result c = 16,14 cm.

How to calculate the cosine of any angle?

We have two options to calculate the cos(x) of an angle x. First, we can use a unit circle to calculate it. On the other hand, we can use cosine law. Let’s look at the first option. As stated, we use unit circles or the most common value tables. This is because the unit circle has all the most important values for trigonometric functions. Below is a figure of the unit circle.

Unit circle
Figure 3: Unit circle

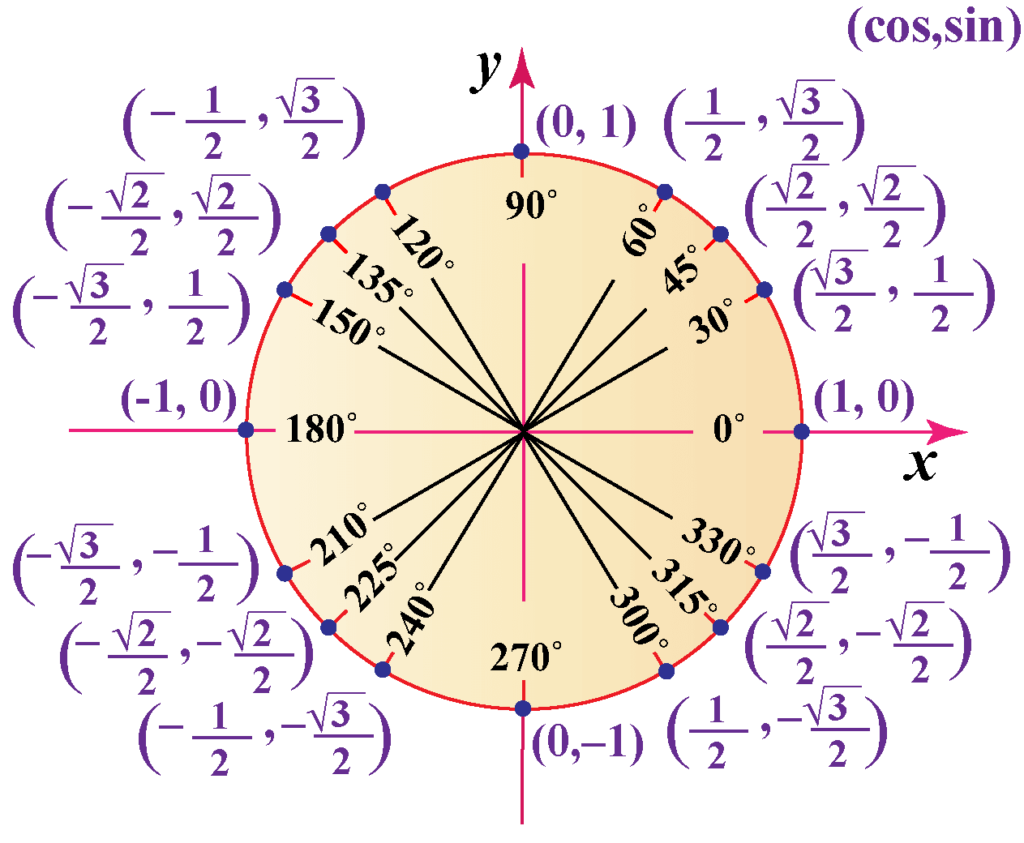
Problem: What is the value of the adjacent side of the angle x = 30 degrees. Hypotenuse is given as h = 36 cm. We must calculate the adjoining side in this given task, which we will mark as side a. 

a = h \times \cos(x) = 31,17 \; cm

Another way to solve any problem (including right and non-right triangles) is using the cosine rule.

Let’s solve a problem. Problem: In a non-right triangle, two sides are 20 cm and 30 cm. The angle between these sides is 60 degrees. Calculate the remaining side. First of all, let us mark sides a, b, and c with values of 20cm, 30cm, and the side we are looking for respectfully.

c=\sqrt{20^2+30^2-2\cdot20\cdot30\cdot \cos(60)}=26.45 \;cm

We get that the side c equals 26,45 cm. From this example, we can notice how powerful the cosine rule is.

Applications of the cosine function

Cos(x), and trigonometry in general, are used in many fields. Most commonly, it is used in game development and navigation. For example, a popular game called “Minecraft” heavily relies on trigonometric functions to estimate the distance to ores, start point, etc. 

As one of the most common trigonometric functions, cosine is related to all trigonometric functions. For example Tangent is defined as sine(x) over cosine(x). So we can get cosine if we know sine and tangents. Other functions such as cotangent are related to tangent, so they are also related indirectly to cosine. Sometimes, we can switch cosine with tangent if it makes problem-solving easier.

Example: How to use a Cosine Calculator?

You can use our Cosine Calculator on this website, or download our app from the Google play store or Apple store. Next, in the search bar, enter “Cosine calculator.” Once the app finds an appropriate calculator, the app will direct you to its main page to calculate different values for cosine. After pressing calculate, you will get the results and steps to solve the problem yourself.