The sine (or sin) function calculator helps you to calculate any sine value. We have a complete step-by-step solution on how to calculate sine. In trigonometry, a branch of algebra, we use sine to estimate functions. Sine is a simple-periodic function, so its use approximates more complex functions is the essential subject of study. Trigonometry studies angles, relationships between angles and sides, and periods of sine and cosine.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is a sine function?
Sine function, most commonly defined as the length of the opposite side divided by hypotenuse, is an essential function in graphing and signal technology. As a simple-periodic function, it can describe the most complex shapes.
As one of the most basic functions in trigonometry, it also has inverse values. For example, the inverse value of sine is arcsine, or sine^(-1). For the inverse sine function, we trade the x-axis and y-axis. The function that returns the angle corresponding to a number is the definition arcsine.
To sum up, sine is a function of the opposite side divided by triangles hypotenuse. It is important to note that we can only calculate sine for triangles. In most applications, we are calculating the size of simple right triangles. Right triangles, by definition, are triangles that have one angle equal to 90 degrees. Therefore, the sum of the two remaining angles must be 90 degrees.
Throughout history, Egyptians utilized sin to calculate the heights of buildings, Earth’s surface & circumference, etc. As we can see, sin has great importance in mathematics. Today, sine is mainly implemented in electronic devices rather than for calculating heights of buildings mannualy.
For example, if we have a right triangle with one of two remaining angles equal to 30 degrees. The last angle must be 60 degrees.
\alpha\;+\beta\;+90\;=\;180
\alpha\;=\;180\;-90\;-\beta\;=\;90\;-30\;=60\;degrees
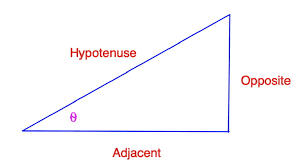
In the right-angle triangle depicted below, we can conclude what sides are opposite and adjacent. So, for example, if we are looking for sine of a right triangle, we can always use a sketch of a right triangle.
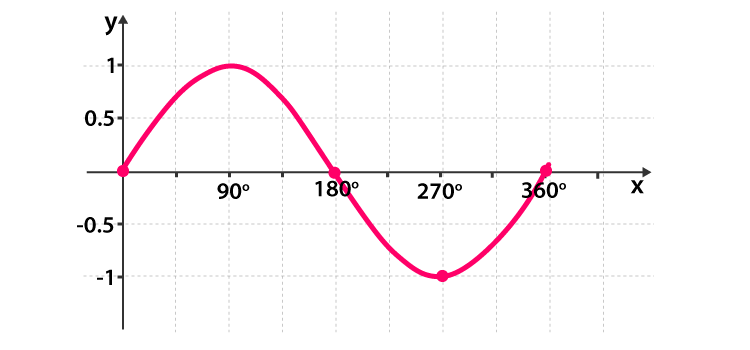
Sine graph and table
The sine graph is a simple periodic graph. By periodic, we mean that it has the same values after a particular time has passed. In trigonometry, by period, we understand a value after which the values repeat. Specific limitations bind these graphs. For example, sine has a codomain of [1,-1]. The same can be said for cosine. On its x-axis, better known as domain, the sine value ranges from the negative infinitive to positive infinity. The graph for sine is shown below.
In retrospect, both sin and cos have fundamental values we remember by heart or unit circle. The table of sine values or most important sin(x) values range from zero to two pi, where pi is a constant equal to 3.1415.

Sin(x) is zero for angles of x = 0, 180, 360 degrees. We write this fact with the following formula: sin(x) = 0 = 0 + k*pi. Where k = 1,2,3… , and pi is a constant.
Sin(x) has value of 1 for x = pi/2 + 2kpi. Most notably, we can represent sine with a unit circle. The unit circle has all the most important degrees and their values for cosine and sin. It is widely used for quick alter calculating degrees, so it would be a good idea to learn it by heart.
How to calculate the size of an angle?
When given a task to calculate the sin(x) of a given angle, where x is given in degrees, we should first sketch the triangle. One example we are going to solve is a right-side triangle. Let’s say we have to calculate the size of a given angle. Angle theta is 30 degrees. If we go back to our unit circle, we can conclude that it is, in fact, a standard angle. Sin(30) of 30 degrees from the unit circle is one-half. However, we must transform if we are given a different value not common in the unit circle. Let’s go back to our sine formula. To emphasize, sin(x) equals the opposite side divided by hypotenuse.
sine(x) = \frac{Opposite}{Hypotenuse}Problem: Calculate sine of 630 degrees. We cannot go to the unit circle without first transforming the angle. If we subtract 360 degrees (a full circle is 2pi radians or 360 degrees) from the given angle, we get 270 degrees which is a typical angle. In retrospect, we can write our angle as 360 + 270 degrees. Now we are looking for an angle of sin(270 + 360).
Note: We use an addition formula for trigonometric functions in this task.
sine(\alpha + \beta) = sine(\alpha)*cosine(\beta) + sine(\beta)*cosine(\alpha)
Now we have our value given as:
sine(270 + 360) = sine(270)*cosine(360) \;+\;sine(360)*cosine(270)
sine(270 + 360)=sine(270)\;+\;0=sine(270)
Sine curve – sine waves
Sine wave, or curve, is a periodic smooth waveform oscillating between two central values (-1 and 1). These values also represent their minimum and maximum values. Waves oscillate in specific periods. Usually, these periods are marked as T. T represents a value of 2*pi. So for a complete oscillation or a whole period, we use 2*T or 2pi. In the following figure, we have a visual representation of waves.
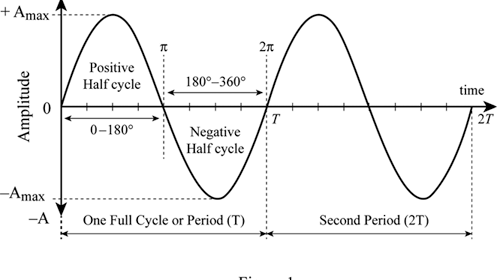
Applications of the sine function
We use sine function, mainly its waves or waveforms, primarily for electronic devices, radio waves, perfecting musical tones (autotune), electrical currents, etc.
Another application of trigonometry, specifically sines, is calculating the height of buildings, aviation, criminology, etc. For example, in criminology, trigonometry is often used to determine the trajectory of a bullet. We can estimate the shooter’s exact spot when the bullet was fired with trigonometry. Another example would be navigation. Ancient sailors used trigonometry to figure out their exact location. They would look at stars and approximate their angle compared to their current location.
Related trigonometric functions
Six most used trigonometric functions are used in trigonometry. Their names are as follows: sines, cosine, tangent, cotangent, secant, and cosecant. All of these are connected or related in some way. For example, tangent equals sin(x) divided by cosine, while cotangent is the opposite. Cotangent is equal to cosine divided by sin(x). These functions are used depending on problems requirements. For example, if we are given two sides(opposite and adjacent), we will use the tangent function or cotangent.
Head to this Cofunction Calculator, to learn more about related trigonometric functions, and also there is our Law of Cosines and Law of Sines Calculator.
Sine calculator
The sin(x) calculator helps you calculate sin(x) for any value of an angle easily. It includes step-by-step instructions on how to solve a problem manually. A graph is also drawn. First, install our CalCon application from google play. In the search bar, enter “sine.”
Next, input the value of the angle. Also, a graph will appear just below the answer to your problem. Step-by-step instructions are also displayed.
