Law of Sines Calculator

Our Law of Sines Calculator comes in help when working out problems with angles or side lengths. We’ll go through the law of sines formula and offer you a list of situations when this rule might come in handy. You may now answer various trigonometry problems with the help of this calculator (more elaborate than the Pythagorean theorem).

This calculator calculates unknown values of a figure using the law of sines. You must input three known values in order to compute the unknown values. Some of the calculation options are redundant, but they are still supplied for accurate letter designations. If you want to know how to find the gradients and margins of a triangle, please check out our Triangle Angle Calculator of geometry, it can be very useful in solving triangles.

Law of Sines

The law of sines provides the math link between an oblique triangle’s sides and angles (non-right triangle). The laws of sines and the law of cosines in trigonometry are key principles for solving a triangle. The law of sines definition (sine rule) states that the ratios of a triangle’s side lengths to the sine of its respective opposing gradients are equal. In the next parts, we’ll look at the formula and how to prove it using solved instances.

The rule connects the ratios of triangle side lengths to their opposing angles. For all three sides and opposing gradients, this ratio stays constant. Using the needed known data, we may use the sine rule to calculate any triangle’s missing gradient or side. The diameter of the circumcircle of one triangle is equal to the ratio of the side and the corresponding angle.

History

The spherical rule of sines was found in the 10th century, according to Ubiratàn D’Ambrosio and Helaine Selin. Abu-Mahmud Khojandi, Abu al-Wafa’ Buzjani, Nasir al-Din al-Tusi, and Abu Nasr Mansur are all said to have written it. Ibn Mudh al-The Jayyn’s book of unknown arcs of a sphere, written in the 11th century, the general geometry and math law of sines.

Nasr al-Dn al-Ts subsequently articulated the plane rule of sines in the 13th century. He stated the law of sines for flat and spherical triangles in his On the Sector Figure and presented evidence for it. “The Law of Sines is truly Regiomontanus’ basis for his solutions of right-angled triangles in Book IV, and these solutions are in turn the grounds for his solutions of general triangles,” according to Glen Van Brummelen. Regiomontanus was a German geometry mathematician who lived in the 15th century.

Any triangle’s area T equals one half of its base times its height. When one of the triangle’s margins is chosen as the base, the triangle’s height is calculated as the length of another side multiplied by the sine of the gradient between the chosen side and the base.

Law of Sines Formula

The law of sines formula is utilized to link the lengths of a triangle’s sides to the sines of consecutive angles. It is the ratio of the length of one of the triangle’s sides to the sine of the gradient created by the other two borders.

Apart from the SAS and SSS triangles, the law of sine formula is applied to any triangle. There are so many equations for the law of sines. But that many equations can be very difficult, so we will provide you with the easiest one, for better understanding. So the law of sines equation is:

\frac {a} {\sin(\alpha)} = \frac {b} {\sin(\beta)} = \frac {c} {\sin(\gamma)}

Where:

• a, b, and c are the lengths of the triangle,
• α, β, and γ are angles of the triangle.

Our calculator will provide you with a few types of triangles.

ASA Triangle

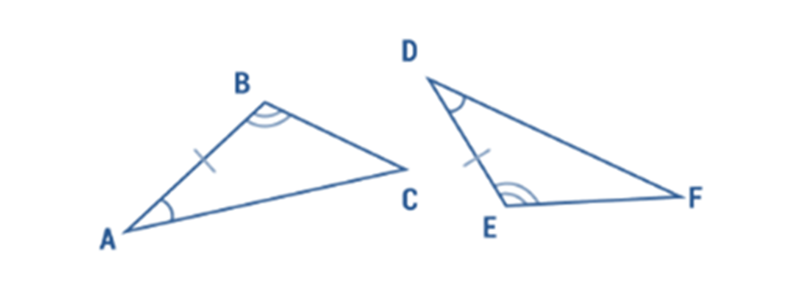
So, suppose any two angles and the included side of one triangle is congruent to two angles and the included side of another triangle. In that case, the two triangles are congruent, according to the Angle-Side-Angle Postulate (ASA). The ASA is used to argue that triangle ABC is congruent to triangle DEF, as seen in the diagram down.

AAS Triangle

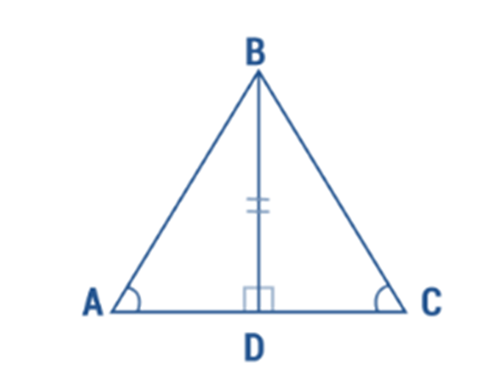
The Angle-Angle-Side Postulate (AAS) states that if two gradients and a non-included side of one triangle are equivalent to two angles and a non-included side of another triangle, the two triangles are congruent. The AAS Postulate demonstrates that triangle ABD is congruent to triangle CBD, as seen in the accompanying illustration.

SSA Triangle

The acronym SSA stands for side – side – angle. t refers to a triangle having two known lengths and one known angle that is not between the two sides. We can work out the remaining side and the other two angles if we have this much information.

For example, consider a math triangle having area of a, b, and c sides. Angle A is the opposite side of a angle B is the opposing side of b, and angle C is the opposite side of c. We know that side a is 8 inches long and side b is 6 inches long in this triangle. We also know that A is a 50-degree angle.

Law of Sines Calculator – How to Use?

Begin by defining your problem. You may, for example, know two angles and one side of a triangle and are seeking the other sides. Fill up the blanks on this triangle calculator using the known values. Remember to double-check whether you used the right symbols to represent the margins and angle values.

Given two angles and a side, the law of sine is used to calculate the remaining sides of a triangle. Triangulation is the term for this method. We can also use it when two sides and one of the non-enclosed gradients are specified. However, in other circumstances, such as the ambiguous example, the triangle cannot be uniquely identified by the available data. We get two alternative values for the enclosed angle.

Enter the opposite side b, then another angle-side pair such as A and an or C and c to compute any angle, A, B, or C, say B. The side gradient (SSA) approach is used in the calculations. The law of sine is only used to finish the calculations for other unknowns. Enter the opposite angle B and then another angle-side pair such as A and an or C and c to compute any side, a, b, or c, say b. The calculations are done using the angled side (AAS) approach, and the law is only used to finish the calculations for other unknowns.

Wow, this calculator is really awesome!

Law of Sines Calculator – Example

Let us now provide you with an example of how to calculate it. So let’s solve this area. First put in the values we know:

• Choose the rule you want to apply – for the sake of example let’s say it’s a/sin(α) = c/sin(γ)
• Input the side a = 7 cm, α = 35 degrees; side c = 10 cm
• Unknown is the γ, and we obtain the result γ = 55,024 degrees

Try out this very useful calculator with your own examples.

FAQ