Trigonometry is a science that focuses on studying triangles and their relations. Due to its frequent use in sciences such as engineering, astronomy, or navigation, we present our Secant calculator. A secant or abbreviated sec calculator binds to the sec function, which is less valuable than other trigonometric functions. This way, we will introduce you to the definition of a secant, explain how to find a secant and how you can calculate it all using our calculator.
Sec in math: the secant definition
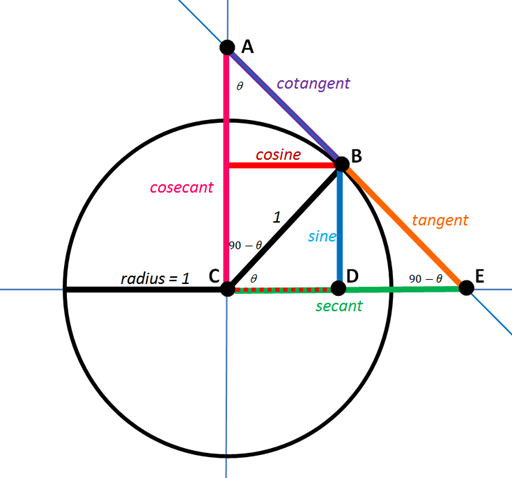
Since we are talking about trigonometry, we need to know what it studies as a science. In trigonometry, we can find explanations for six ratios and functions, which are: sine θ, cosine θ, tangent θ, secant θ, cosecant θ, and cotangent θ. All trigonometric functions serve to describe the relationships between the sides of triangles. The first three functions are the basic ones from which the remaining three functions and ratios are derived. The secant is obtained by deriving from the cosine function. By definition, you can define secant in a right triangle as the ratio of the length of the hypotenuse of a triangle to the length of the adjacent side of the triangle. If we do not have data on the size of the triangle itself, as long as the angle is unchanged, the value of the sec function will remain the same. There are certain shortcomings of these functions. You can calculate the sec function only when we have an angle between 0 and 90 degrees or between 0 and π / 2 expressed in radians because it is a right triangle. There is a way to turn a secant definition into a two-dimensional Euclidean space or plane, whereas you can apply it to accurate and even negative angles.
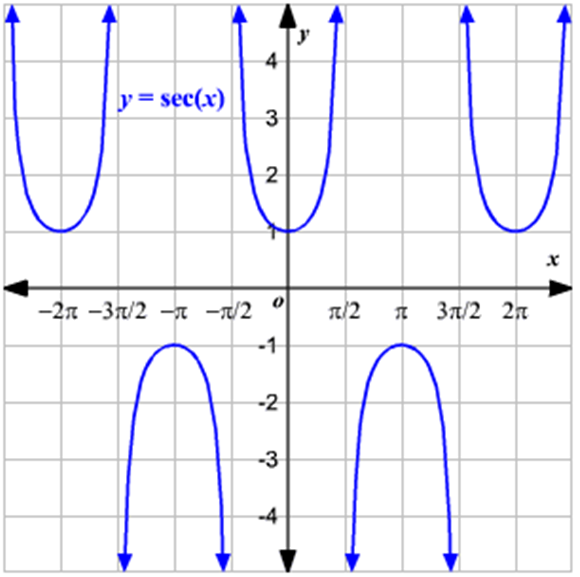
Sec function graph, the domain of secant
We still use trigonometric ratios as functions of variables with which we can measure angles. Depending on the need, you can express the secant measures in degrees or radians. Any angle with a dimension greater than 2π radians or less than zero is equal to an angle with a dimension between 0 ≤ π < 2π. This relation and equality show us that all trigonometric functions behave periodically. In the following graphic representation of the secant, we can see how it moves. When it comes to the secant domain, it looks like this:
y = sec(x) = \frac{1}{cos(x)}These are real numbers, with the value of cos (x) equal to zero, and the range ranges from y ≤ -1 or y ≥ 1.
How to find the secant? Alternative secant formulas
If you are wondering how to find a secant, you need a right triangle for that. For an example of manually calculating and defining a secant, you need to know the value of the hypotenuse of the triangle and the adjacent side of the triangle, after which it is sufficient to enter the values in the formula below:
sec(x) = \frac{c}{b}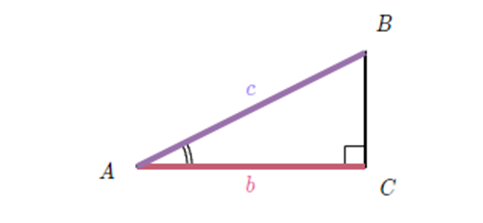
Following the formula, we conclude that the secant is directly related to the cosine function. You can obtain the secant value by calculating the reciprocal of the angle cosine. Accordingly, we can present the following formula:

The table gives us an overview of the direct connection between these two functions and introduces us to the cosecant. It is a trigonometric function obtained by dividing the length of the hypotenuse of a triangle by the length of the opposite side. Cosecant is also known in the literature as “csc”. When you want to calculate this function on a calculator, you probably won’t be able to because most electronic and modern calculators don’t have that capability. Just as the secant represents the reciprocal of the cosine, the secant represents the reciprocal of the sine, which you can calculate using the following formula:
csc(x) = \frac{c}{a}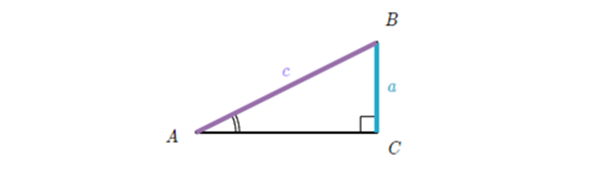
Basic Properties of Secant Function
It is necessary to determine the quadrant in which a certain angle lies to define the sec function’s basic properties. We will best illustrate this with the example of a circle. From the graphs below, we can conclude that the value of the secant in the first and fourth quadrants is positive. In contrast, it is negative in the second and third, which further confirms the statement about its periodicity. We will say that a function is periodic when it satisfies a particular horizontal shift (P) and gives the result of a function equal to the initial function. We can show this as follows:
f(x+P) = f(x)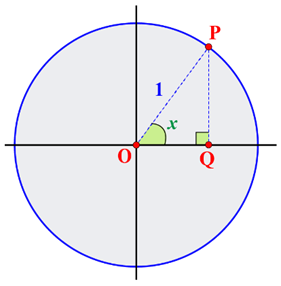
From this graph you can find Secant as following:
sec(x) = \frac{OP}{OQ} = \frac{1}{OQ}You can also find the values read from the circle in the table for secant, which shows all the angles together with their values expressed in degrees or radians.
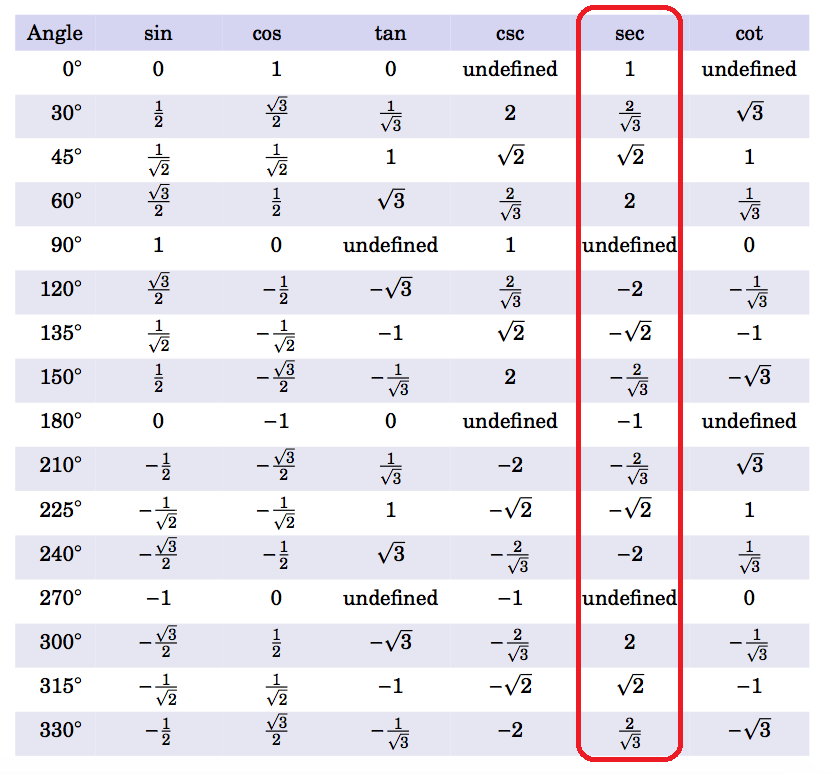
Range and Domain of Secant Function
It is essential to define the rank and domain of the sec function. It is centered on the y-axis, and this position helps us determine its symmetry.
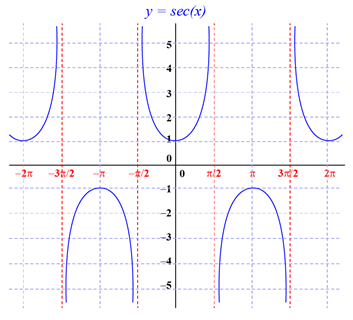
From the graphs, we read that the domain of the secant includes all real numbers except the (π/2) + ηπ, while the range of the secant is a set of all real numbers that are greater than or equal to 1. We can write this in the following way:
Domain of secant: R except (π/2) + ηπ
Range of secant: (−∞,−1]∪[1,∞)
Example: using the secant calculator
Let’s say you need to calculate the values of trigonometric functions for different angles. Secant calculator is here to answer all your doubts in a few steps. This calculator works on an elementary principle like other CalCon calculators. It contains one empty field where it is necessary to enter the angle value. After entering the value, the answer will appear immediately. If you want to find the secant yourself, it is enough to follow the formula we presented in the text above, using the triangle and angles. In the following example, we can see how the secant calculation is done using the formula:
sec (780) = \frac{1}{cos (780)} = \frac{1}{cos(60+2\cdot 360)} = \frac{1}{cos(60)} = \frac{1}{\frac{1}{2}} = 2