Hi folks, if you know the lengths of the other two sides of a right triangle, our Pythagorean Theorem Calculator will determine any missing sides’ length. Calculating the hypotenuse is part of this. The longest side of a right triangle is the hypotenuse, which is the side opposite the 90 degree angle. The hypotenuse formula, we may use it to get this side when solving for the hypotenuse.
Remember that a right triangle is the one with a 90-degree angle. Because the value of the angles of any triangle added together must be 180 degrees, the other two angles must similarly total 90 degrees. Make sure to see other related calculators on our site, such as 45 45 90 Triangle, 30 60 90 Triangle Calculator or Area calculator.
Take a look other related calculators, such as:
- Phase shift calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is the Pythagorean Theorem – Definition?
The Pythagorean theorem states and describes how the three sides of a right triangle are related. Pythagoras defined the square of the hypotenuse (length opposite of 90 degree angle) as the sum of the squares of the other two sides of that triangle. Let’s look at it, its derivations, equations, and some solved instances.
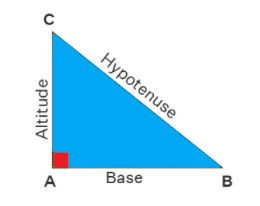
If a triangle is a 90 degrees one, the square of the hypotenuse equals the sum of the squares of the other two sides. Consider the triangle ABC, in which:
BC^2= {AB^2+ AC^2} The hypotenuse is BC, the base is AB, and the altitude (height) is AC. It’s worth noting that the hypotenuse is a triangle’s longest side. Our calculator will provide you with all information and data you need.
History of Pythagoras Theorem
So the Pythagorean Theorem was one of the first theorems known to ancient societies. Pythagoras, a Greek mathematician, and philosopher is its founder. In Cortona, a Greek seaport in Southern Italy, Pythagoras founded the Pythagorean School of Math. Many of his contributions to mathematics are ascribed to him. However, some of them may have been the work of his pupils.
Although Pythagoras popularized the theorem, there is enough evidence to suggest that it existed in other cultures 1000 years before Pythagoras. The earliest evidence originates from the Old Babylonian Period, between the 20th and 16th centuries B.C.
According to legend, Pythagoras was so overjoyed when he discovered the theory that he sacrificed an ox. However, Pythagoras and his successors were profoundly upset by the subsequent revelation that the square root of 2 is irrational and cannot be stated as a ratio of two numbers. They were adamant that any two lengths were integral multiples of the same unit length.
There have been several efforts to conceal that the square root of 2 is irrational. The individual who revealed the knowledge is even claimed to have perished at sea.
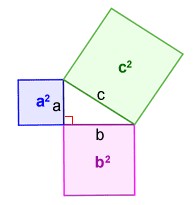
Pythagoras Theorem Formula
The square of the hypotenuse is equal to the sum of the squares of the sides of a right triangle. We can use the hypotenuse formula to describe Pythagoras theorem. If the hypotenuse is c and the sides of a right triangle are a and b, the equation is:
c^2= {a^2+ b^2} Maybe our Triangle Area Calculator can help you to learn more, or this this post about the Right Triangle.
Pythagorean Theorem: Algebraic Proof
When two triangles’ two sides are equal to each other’s two sides, and the angles encompassed by those sides are equal, the triangles are congruent (side-angle-side). A triangle’s area is half of the area of any parallelogram with the same base and height.
It uses a trapezoid instead of a square, which may be constructed by bisecting along with one of the inner square’s diagonals, as shown in the diagram, from the square in the second of the above proofs. The area of the trapezoid may be estimated as half of the square’s area, which is:
Area \, of \, Trapezoid=\frac {1}{2} \times (b+a)^2Pythagorean Triples
Pythagorean triples are a collection of three positive numbers that fit into the formula, which is a2 + b2 = c2, where a, b, and c are all positive integers. So the longest side of the triangle is known as the hypotenuse, or ‘c,’ while the other two legs of the right triangle are ‘a’ and ‘b.’ The Pythagorean triples are denoted by the symbols (a, b, c). The most well-known Pythagorean triple example is (3, 4, 5).
The Pythagorean triples set is infinite. The earliest Pythagorean triples are (3, 4, and 5). We can create a few extra triples by scaling them up in the following way. Taking values for n allows us to make as many triples as feasible.
Table of Pythagorean triples
| n | (3n, 4n, 5n) |
| 2 | (6, 8, 10) |
| 3 | (9, 12, 15) |
| 4 | (12, 16, 20) |
Pythagorean Theorem Calculator – How to Use?
You’ll be able to utilize this incredible Pythagorean Theorem Calculator if you follow these simple steps.
- Fill in the formula with the two lengths you have. Let’s say you know a = 4, b = 8, and you want to calculate the length of the hypotenuse c. Solve it now.
- After plugging the numbers into the formula, we get 42+ 82 = c2.
- To obtain 16 + 64 = c2, square each word.
- To obtain 80 = c2, combine comparable words.
Just simply enter the values in our calculator, and let it calculate for you!
Pythagorean Theorem Calculator – Example
A right-angled triangle’s hypotenuse is 16 units long, while one of the triangle’s sides is 8 units long. Substituting the provided dimensions into the calculator, consider the given side of a triangle as the perpendicular height = 8 units. Solve it:
Hypotenuse^2= {Base^2+ Height^2} 162 = {B^2 + 82}B^2 = {256 - 64}B = {\sqrt{\smash[b]{192}}} = 13.856FAQ
What is the Pythagorean theorem used for?
The Pythagorean Theorem is a handy method for determining the side lengths of a right triangle by adding the areas of three intersecting squares. Moreover, this theorem is a very helpful technique that serves as the foundation for more difficult trigonometry ideas, such as the inverse. There are also other uses in real world.
How to solve the Pythagorean theorem?
What is the square root? We can define square root as the sum of the sides squared is the length of the hypotenuse. Try using the formulas above for solution.
Who created the Pythagorean theorem?
In Cortona, a Greek seaport in Southern Italy, Pythagoras founded the Pythagorean School of Math. Many of his contributions to mathematics are ascribed to him. However, some of them may have been the work of his page pupils. Pythagoras’ most renowned mathematical contribution is the Pythagorean Theorem.
How do you find the missing side of a triangle using the Pythagorean theorem?
In a right triangle with c as the longest side, the theorem asserts that a2 + b2 = c2. You may use this equation to calculate the length if you know the lengths of the other two sides. The illustration depicts two right triangles with one side lacking their measure.
Is the Pythagorean theorem only for right triangles?
We may use the Pythagoras’ theorem to determine whether or not a triangle has a right angle because it only applies to right-angled triangles.
