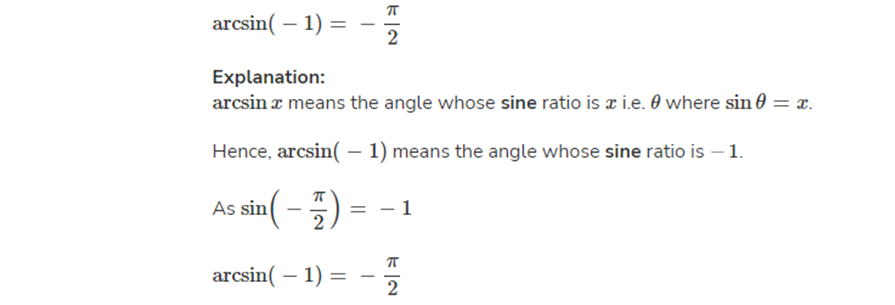The mathematics of trigonometry is complex and, at times, confusing. To make this topic understandable to you, you will get a detailed explanation through this article of inverse sine, trigonometric functions, and other relationships. Accordingly, we present you with our arcsin calculator and the principle of operation, which will greatly help you in the calculation.
What is arcsine?
The arcsine is a trigonometric function in math that produces a final result in the range of -1 to 1. The inverse of the sine function calculates the arcsine. The function is typically used to convert the results of the arccosine function to degrees. It is commonly used in engineering, especially in signal processing. It is sometimes called the “inverse sine” or “arcsine law.” Each trigonometric function has its inverse function, which works the other way around. How can we conclude that when we see “arcsin A,” we understand it as “the angle whose sin is A”.
How to calculate arcsin?
As a math function, it is needed in some applications, such as calculating the angle of refracted air. You can use the following formula to calculate arcsin:
A = arcsin (sin (x))Arcsin can also be calculated using the following table, for example, if sine 45° is 0.7071068:
sin (45°) = 0.7071068
arcsin (0.7071068) = sin-1 (0.7071068) = 45°
and then the arcsin of 0.7071068 is 45°
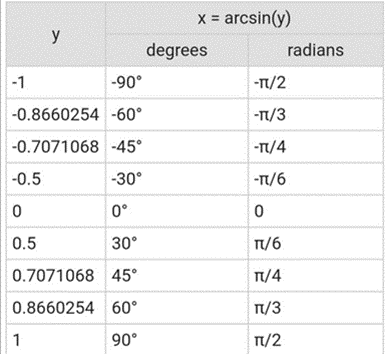
The arcsin x is the graphical representation of the inverse trigonometric function. The graph is a continuous curve with a steep slope, going from 0 to 1 as x increases from -π/2 radians to π/2 radians.
However, the Arcus sine is an inverse function of this restriction, which is valid.
arcsin \equiv sin^{-1} : \left [ -1,1 \right ] \rightarrow \left [ -\frac{\pi }{2}, \frac{\pi }{2} \right ]Based on this formula, we can conclude that the function is strictly increasing, continuous, odd, and has no symptoms.
Inverse sine, trigonometric functions, and other relationships
You can apply trigonometric functions to different angles, including negative and large angles. If we talk about the inverse function, we know that there are an infinite number of angles whose sine is the same, and that’s where the problem comes from. For example, 45 degrees and 360 + 45 degrees will have the same sine. To solve this problem, the set of these inverse trigonometric functions is limited so that the inverse functions are one-on-one, which tells us that there is one result. The relationship between arcsine and trigonometric functions can bring you closer to this topic to make it more transparent. The arcsine is a trigonometric function that converts an angle from the side of a right triangle to an angle on the unit circle. Also can be used to find the value of the sine of an angle not in the first quadrant. This trigonometric function is commonly used in geometry and trigonometry.
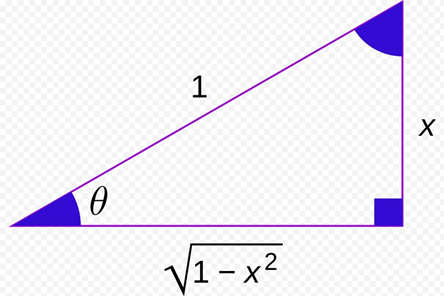
What is important to emphasize when it comes to the inverse sine function is that it is a finite sine function, which means it is not the whole sine function.
Relationships among the inverse trigonometric functions:
arccos(x) = \frac{\pi }{2} - arcsin(x) arcsin(-x) = - arcsin(x)Example of using the arcsin calculator?
Arcsin calculator provides an easy way to calculate arcsin without any hassle. These types of calculators can help you find the inverse of arcsin’s trigonometric function. With the help of this trigonometric function, we can also find the angles of a right triangle.
for α:
sin(\alpha) = \frac{a}{c} \Rightarrow \alpha = arcsin (\frac{a}{c})for ß:
sin(\beta) = \frac{b}{c} \Rightarrow \beta = arcsin (\frac{b}{c})If we have two values given in a right triangle such as a = 4 and c = 8, and we want to find the value of the angle a:
When we want to find arcsin, we enter a value. In our case, it is 4/8 and what we must not omit is that the value will be between -1 and 1, and in a few steps, we find arcsin, which in this example was 4/8 = 0,5, which means the angle of 30 degrees.
How to find arcsin without a calculator?
With the use of a calculator, we can quickly come up with the calculation of arcsin. However, it would look like this when we work without a calculator, as shown in the following example.
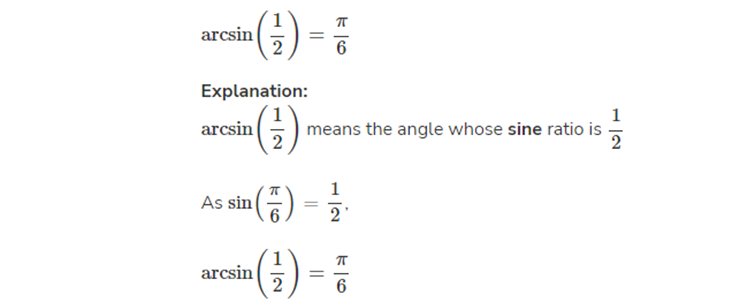
or in example number 2: