The Polar Coordinates Calculator is the perfect way to do quick calculations when working with this kind of coordinate system. It can be difficult to see the relationship between angles and radius with a standard calculator. It is not a linear transformation. The calculator solves this problem by displaying angles and radius in a circular arrangement.

This calculator can also convert coordinates from polar to rectangular, or vice versa. If you are interested in calculating a rectangle, you can do equations with our Rectangle Calculator. This article will briefly explain both types of coordinates and the formula for a fast conversion.

Take a look other related calculators, such as:

Polar Coordinates – Definition?

Polar coordinates are in a two-dimensional coordinate system.  The polar coordinate system comprises two perpendicular lines, one horizontal and one vertical. The horizontal line is called the r-axis, and the vertical line is called the theta – θ.

You can read the coordinates as (r, θ). This coordinate system is based on measuring the distance of a point from a fixed point on a circle.

Polar coordinates are a method of complex graphing numbers in r = (a, b), where a and b are real numbers. This coordinate system has the advantage of not requiring any complex numbers to be reduced to their rectangular form.

Polar vs. Cartesian (Rectangular) Coordinates

You can use the polar coordinate system in two dimensions, where you draw a line from the beginning to the end to create a coordinate system. This is the point at the intersection of the line and the axis. The measure of the angle of the x line is always horizontal. This coordinate system represents two numbers, the distance from the origin and the angle of the line x.

It is important to emphasize that the pole is the source of the system. To find the polar coordinates, you need to draw a line that will merge with the pole. In that case, the coordinates are the length of the line p, as well as the angle contains that forms the polar axis.

A Cartesian coordinate system is a grid that you can create in any number of dimensions. Cartesian systems use linear distances. You can identify points by an ordered pair of numbers, and you can use both to determine your online location. The first number is the x-coordinate, and it determines the horizontal position on the grid. The y-axis is a vertical line that runs from top to bottom. The distance of a point from the origin you can call as magnitude. The magnitude of a point is always a positive number.

Converting Cartesian coordinates to polar coordinates is making a point (x, y) and converting it to (r, θ). This conversion is often necessary when solving math problems that involve the conversion of rectangular to polar coordinates.

Relation between polar and Cartesian coordinates
Relation between polar and Cartesian coordinates

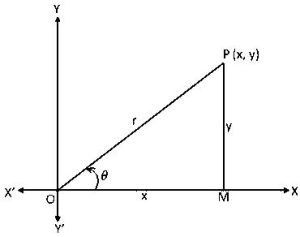
Polar to Rectangular Coordinates – Formula

The polar to Rectangular Coordinates formula is a grid conversion tool that allows users to convert a polar coordinate to a rectangular coordinate. This is an excellent tool for students in math classes learning about these systems. To convert from polar to rectangular coordinates, use the following formulas:

x = R \cdot \cos \theta

y = R \cdot \sin \theta

Rectangular to Polar Coordinates – Formula

The Rectangular to Polar Coordinates – Formula is a helpful tool for calculating polar from rectangular coordinates and other equations. You can use this formula in science, engineering, and mathematics:

r=\sqrt{x^{2}+y^{2}}

Radius r is the distance from the origin, and θ is the angle from the x-axis.

\theta = \arctan \frac{y}{x}

where:

(x, y) – represent Cartesian coordinates;
(r, θ) – represent polar coordinates.

The following restrictions apply to polar coordinates:

  • r – should be equal to or greater than 0
  • θ – the position must be within the range [−π, π]

Polar Coordinates Integral – How Do You Integrate?

Polar Coordinates Integral is a simple way to solve integrals of the form. You can use integral to calculate the area of a region enclosed by two curves. The region may be rectangular or elliptical. You can define a region with two polar curves, r (θ) and r ‘(θ).

You can use the polar coordinate integral to calculate the area of a region enclosed by two polar curves. The region may be either rectangular or elliptical.

Area in Polar Coordinates

You can use the polar coordinate system to graph circles, ellipses, and other conic sections. Also, you can solve problems involving the area of circles. The coordinates are written in the form r, θ, where r is the distance from the center of the circle to the point, and θ is the angle measured from the center to the point. You can identify points in a complex plane by their real part and their imaginary part.

If you need to visualize the coordinates, try using a protractor to create a circle with a radius of 1 unit. Draw an X at the center of the circle. Label the X as the pole and the area around the X as the equator. 

  • At point P on the equator, your coordinates are (0,1). 
  • If you are at point Q on the equator, they are (1,0). 
  • If you are at point R on the equator, they are (1,1).

The area in polar coordinates is a particular type of plane geometry that represents the plane with a circular boundary. The center of the circle is the pole, and the circle’s circumference is the equator.

Area with Polar coordinates
Area with Polar coordinates

Polar Coordinates Calculator – How to Use?

The polar coordinates calculator helps mathematicians calculate the coordinates of a point in the Cartesian plane. The app is straightforward to use. The user is given the option to input the point coordinates in Cartesian or polar coordinates and calculate the other ones.

For Cartesian input coordinates, the user inputs the x and y coordinates. To input polar coordinates, the user inputs the angle and radius, thus you get your results in no time.

Polar Coordinates Calculator – Example

To convert from Cartesian to Polar, we solve a right triangle with two known sides. We will best explain this in the following example.

For example, you need to calculate what does (11, 4) represents in polar coordinates? You can use the equation for Pythagoras Theorem to find the long side, or the hypotenuse and it looks like this:

r=\sqrt{x^{2}+y^{2}} = \sqrt{11^{2}+4^{2}} = \sqrt{121+16}=\sqrt{137}

But if you are using the Tangent Function to find the angle, it will look like this: 

\tan \theta = 4 \div 11 =19.8 \degree

Related equation to express measures in Cartesian coordinate system (x, y), uses a right triangle with a known long side and angle, and then it looks like this:

x=12\cdot \cos 19.8 \degree = 11.28

In addition, you can use the Sine Function for y.

y=12 \cdot \sin 19.8 \degree = 4.08

In conclusion, the answer is the point (12, 19.8) is almost exactly (11, 4.08) in Cartesian Coordinates.

To sum up, you should also head to our related Spherical Coordinates Calculator.

FAQ

How do you find polar coordinates?

Finding the equation of polar coordinates is easy with the help of our calculator. Enter the radius, angle, and degrees to convert to polar coordinates. 

How are polar coordinates different from rectangular coordinates?

Rectangular coordinates are coordinates with an x and y-axis. The polar coordinates differ from the rectangular coordinates because they use an angle and radius instead of the x and y-axis.

Can polar coordinates be 3D?

This calculator can be helpful for those who need to graph points on a surface or those who need to solve problems involving 3D space. The user would input the coordinates of the points, and the calculator would graph the points on the surface.

How to convert rectangular coordinates to polar coordinates?

All you need to do is take the x-coordinate and y-coordinate and convert them to their polar equivalents. The rectangular coordinates will be the coordinates on the plane, while the polar coordinates will be the radius vector and angle of the point.