Vector Magnitude Calculator

This Vector Magnitude Calculator is a straightforward tool for estimating magnitude from vector components. In this text, you’ll learn how to find the magnitude of a vector and become familiar with the general magnitude of a vector formula, what is math definition of a vector, how to use this calculator, and more. In addition, you can learn about several physical quantities that are vectors and what their magnitudes tell us towards the conclusion of the essay.

You can also learn more about vectors by visiting our Vector Projection Calculator, and Unit Vector Calculator. In addition, do the vector product with our Cross Product Calculator. There is also this Angle Between Two Vectors Calculator to calculate the angle.
Also, you will learn about trigonometric functions and their use in geometry, 45 45 90 triangle calculator, 30 60 90 triangle calculator. For more geometry and trigonometry related posts and questions, as well as other math articles, explore our database of different calculators like sum and difference identities, and find your answer.

Vector Magnitude – Definition?

A vector’s magnitude is called length or distance between the initial point A and the end point B, like shown bellow.

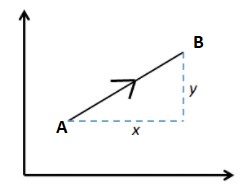
How to find the magnitude of a vector?

A vector is a set of integers that are arranged in a certain sequence. The space’s dimension determines the number of vector components. We frequently work with 3-dimensional vectors with three separate components in practice. The values of the x, y, and z components can be useful in Cartesian coordinates.

When we convert to spherical coordinates, we may utilize the magnitude, which is the length of a vector in its purest form, and the values of two angles, angle θ and angle φ. To put it another way, it’s the three-dimensional distance between a vector’s start and finish points.

A vector’s components can also be complex numbers.

The magnitude of a Vector Formula

Depending on the dimensions of the vector space, the magnitude of a vector |V| can be approximated in a variety of methods. We have the following:

|V|=\sqrt{({x^2}+{y^2})}

|V|=\sqrt{({x^2}+{y^2}+{z^2})}

|V|=\sqrt{({x^2}+{y^2}+{z^2}+{t^2})}

In all circumstances, magnitude is the square root of the sum of vector components to the second power, as shown in the formula for vector magnitude. You may choose the proper formula by changing the dimensions of your vector in this vector magnitude calculator. As a result, the magnitude’s value is always positive, allowing us to quantify it in any experiment using vector quantities.

Also, a vector’s magnitude may alternatively be determined as the square root of the vector’s dot product with itself:

|V| = \sqrt{(V\cdot V)}

Vector Direction and Magnitude

We must be able to know the magnitude and direction of a vector in order to operate with it. The distance formula, or Pythagorean Theorem, is used to calculate its magnitude, and the inverse tangent function is used to calculate its direction. For example, |V|=\sqrt{a^2+b^2} calculates the magnitude given a position vector v = a, b.

Vector Magnitude Calculator – How to Use?

The use of our vector calculators is very easy. To find the size of the vector, do the following:

In the first field, select whether you want a 2D, 3D, 4D or 5D vector display. Next, fill in the coordinates of the vector. And that’s it, the calculator automatically calculates your default data and dimensions.

Vector Magnitude Calculator – Example

To understand how to find the magnitude of a vector in 4-dimensional space, look at this computational example. The vector’s components are

x = 3, \; y = -1, \; z = 2, \; \text {and} \; t = -3 .

x² = 9,\; y² = 1,\; z² = 4,\; t² = 9 ; calculate the squares of each vector component.

We will have:

x^2 + y^2 + z^2 + t^2 = 9 + 1 + 4 + 9 = 23 .

Calculate the vector’s magnitude as the square root of these numbers:

|V| = \sqrt {23} = 4,796 .

Vectors in Real Life

Many physical quantities are vectors, such as force, acceleration, and velocity. Also, the magnitude of a vector is the absolute value of the measured quantity in these circumstances, much as speed is the magnitude of velocity.

Other, more sophisticated ones can be made by calculating the cross-product of two vectors. For example, the cross-product of distance and force vectors is torque.

FAQ