CalCon has developed a tool for calculating Spherical coordinates based on Cartesian coordinates. This can be done using the Spherical Coordinates Calculator, which also allows reverse conversion from Spherical Coordinates to Cartesian 3D Coordinates. All you need to enter are Cartesian coordinates in metric units, after which you will get Spherical coordinates in the form of radius, theta, and phi. Similarly, you can enter Spherical coordinates and get the Cartesian coordinates.
Furthermore, this article will briefly say something about the spherical coordinate system, it’s coordinates and their shapes and formulas, and rectangular coordinates. Then, we will do a few examples of calculations.
On the other hand, take a look at some of our solutions, especially in the field of math, such as the Area of the Right Triangle Calculator, or some in the physics section, such as the Belt Length calculation tool. There is our Three-Dimensional Distance tools as well.
Spherical coordinate system
A coordinate system is a system that allows points on a curve, line, surface, plane, or space to be described using numbers, so-called coordinates. There are several different coordinate systems in mathematics and other fields, such as Cylindrical coordinates, but here we will talk about the Spherical and Cartesian systems.
In math, the Spherical coordinate system is a system for representing a body in three dimensions using three coordinates: the distance of the point from the fixed zero point (radius), the angle that connects the line connecting the point with the origin with the positive part of the z-axis (zenith) and the angle of the same line with the positive part of the x-axis (azimuthal angle).
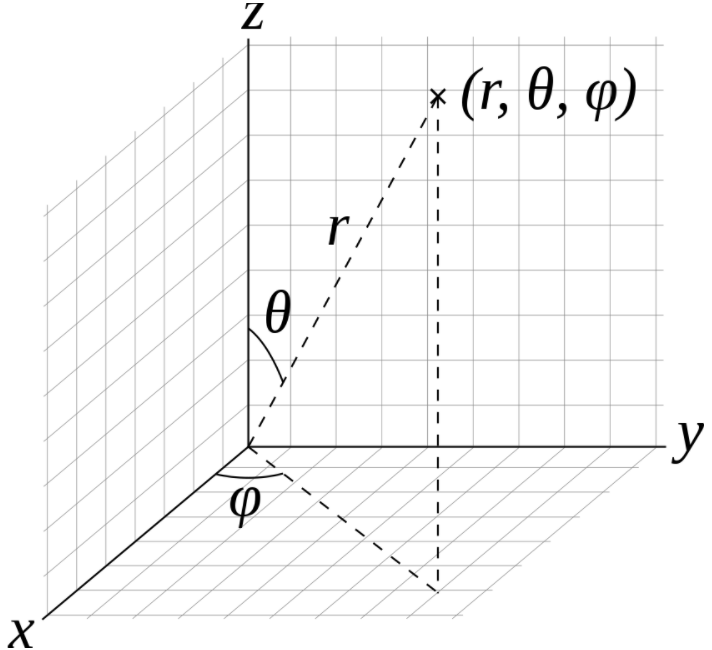
In other words, spherical coordinates (r, θ, φ) are radial distance r (distance to origin), polar angle θ (theta) (angle referring to the polar axis), and azimuthal angle φ (phi) (angle of rotation from the initial meridian plane). The symbol ρ (rho) is also used instead of r.
Each point/shape in space is uniquely determined when the values of above coordinates are limited:
0 <ρ <∞,
–π <φ <π,
0 <θ <π.
Where π (PI) is the math constant. The numeric value of π rounded to 64 decimal places is given below:
π ≈ 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923
But often use only two decimal places, so we get 3,14. The value of π radians refers to 180° (degrees) in angular units, two π = 360°, etc.
Spherical and Rectangular coordinates
Spherical coordinates are a little challenging to understand at the beginning. They determine the position of a point in three-dimensional space based on the distance ρ or r from the origin and two angles θ and φ. If one is known with polar coordinates, then the angle θ isn’t difficult to understand as it is essentially the same as the angle θ from polar coordinates. Azimuthal angle φ is the rotation angle from the initial meridian plane with a positive counter-clockwise direction.
The Cartesian, Rectangular, or Rectangular Cartesian coordinate system in space is determined by three mutually perpendicular directions x, y, z, which intersect at the origin O. The Cartesian coordinates are the abscissa (on the x-axis), the ordinate (on the y-axis), and the applicate (on the z-axis).

Coordinate conversion formula
The mentioned coordinate system is just one of many three-dimensional systems, so there are equations for conversion from spherical coordinates and others, and vice versa. We will show the connection between spherical and three-dimensional Cartesian coordinates in the following text.
To get Spherical coordinates based on the Cartesian coordinates, you need to use the following equations:
\rho = \sqrt {x^2+y^2+z^2}\phi = \arccos \left ( \frac {z} {\sqrt {x^2+y^2+z^2}} \right )\theta = \arctan \left ( \frac {y} {x} \right )Conversely, rectangular coordinates are obtained from spherical ones by these equations:
x = \rho \sin \phi \cos \theta
y = \rho \sin \phi \sin \theta
z = \rho \cos \phi
As you can see, we are mostly dealing here with trigonometric functions, so if you have any difficulties, see this Trigonometric Functions Calculator, or directly you can visit Cosine or Arccos Calculator, to get better information.
Example – Converting Cartesian to Spherical
For example, let’s take the coordinates of a point in a rectangular 3D system, as below:
x = 15000
y = 30000
z = 45000
To convert these coordinates into spherical coordinates, it is necessary to include the given values in the formulas above. However, we will do it much easier if we use our calculator as follows:
- Select the Cartesian to Spherical mode
- Enter x, y, z values in the provided fields
Read the values of the obtained coordinates, and that
- radius r in meters
- θ angle in desired units (radian, degree, etc.)
- angle φ in desired units (radian, degree, etc.)
In our example, the results are as follows:
- r = 56.124,86
- θ = 0,64 rad
- φ = 1,11 rad
Example – Converting Spherical to Cartesian
On the other hand, let’s do the conversion from spherical to Cartesian coordinates. Let’s assume we have the following coordinates:
r = 12.457,00 meters
θ = 0,78 rad
φ = 57,1547°
Our next task is to enter these values in appropriate fields of the calculator, as below:
- Change mod – Spherical to Cartesian
- Enter in field r-value of 12457
- For the θ angle, choose the “rad” units and enter 0,78
- For the φ angle, choose the “deg“ units and enter 57,1547
After that, we get the following results – Cartesian coordinates:
- x = 4.751,59
- y = 7.360,24
- z = 8.855,85
The results are in meters.
FAQ
What is the application of Spherical Coordinates?
We use it to analyze systems with some degree of symmetry about a point, such as volume integrals inside a sphere, the potential energy field surrounding a concentrated mass or charge, or share global weather simulation in a planet’s atmosphere.
What are the Cylindrical Coordinates?
We add a new axis to model the third dimension when expanding the traditional Cartesian coordinate system from two dimensions to three. Cylindrical coordinates provide an extension of polar coordinates to three dimensions.
How to convert coordinates from one system to another?
Usually, many formulas are derived on the web and there are online tools for conversion. To convert the coordinates, you can use online tools or the derived formulas and a calculator.
