In the following text, you will be able to comprehend the meaning, appliance, and geometrical illustration accompanied by the formulas for the perimeter. With only two things on our mind, which are making it simple for our readers to understand and use our calculators, the CalCon team created the Perimeter Calculator. Also, we offer an extensive explanation regarding the topic in the text that follows. So sharpen your mind, dive into the text and see why it is worth checking out our other calculators.

Speaking about them, here are some of our suggestions: area calculator, volume calculator, circumference calculator, angle conversion calculator, and many others. Moreover, we would love it for you to contact us if there is any topic about whom you would like to learn more that we have not processed yet. Because as we like to say, our motto is to be on your service. Finally, do not forget to keep in touch with the newest calculators on our site. We bet you will like it.

Take a look other related calculators, such as:

What is the perimeter?

The perimeter is defined as the sum of the length of all sides of the geometry shape. In other words, it is the length of a line bounding the figure. To clarify, let’s walk through these examples where perimeter calculation is used in everyday life.

One of them is putting a fence around your house and yard. In order to calculate how much material you need to build or assemble your fence, first, you need to know the perimeter of your yard. Or, if you want to put decorative lights around your house, you need to know the house’s perimeter to buy the lamps long enough to cover the walls.

Also, if you are a cooking fan, you encountered that many recipes demand the exact measure of the baking mold, given as the perimeter or diameter. Our calculator enables this only by entering the values for the looking shape’s perimeter.

Definition of the perimeter

The word perimeter comes from Greek, where “peri” means around, and “metron” means measure. Therefore, the perimeter is the measure of the line that goes all the way around the two-dimensional shape. The more precise definition is: ”The perimeter is the length of the line bounding closed geometrical figure.”

How to find perimeter?

The perimeter is the sum of every straight line’s length that forms the figure. When possible and needed, we dissolve more complex figures into parts (straight lines) to make our calculations easier. After taking the measure of each side, we input them into the formula to get the perimeter. This does not apply to circle-shaped figures, whereas their perimeter is called the circumference. However, an easier way is to use our calculator given in the upper right corner of this page.

Perimeter calculator – formulas

Now, we will provide perimeter formulas for some commonly used geometrical figures. While doing the calculation, we need to ensure that the measurements are in the same units. The base SI unit for the length is a meter. Also, we use derived units such as millimeter, centimeter, decimeter, kilometer, and many other prefixes. Furthermore, we will mark the perimeter with the letter P.

The perimeter of a rectangle

The rectangle is a two-dimensional figure with four right angles and four vertices. The perimeter of a rectangle is the sum of the lengths of its sides. Because the rectangle is formed from two sets of two identical sides, the formula for the perimeter of a rectangle is $P=a+a+b+b$ .

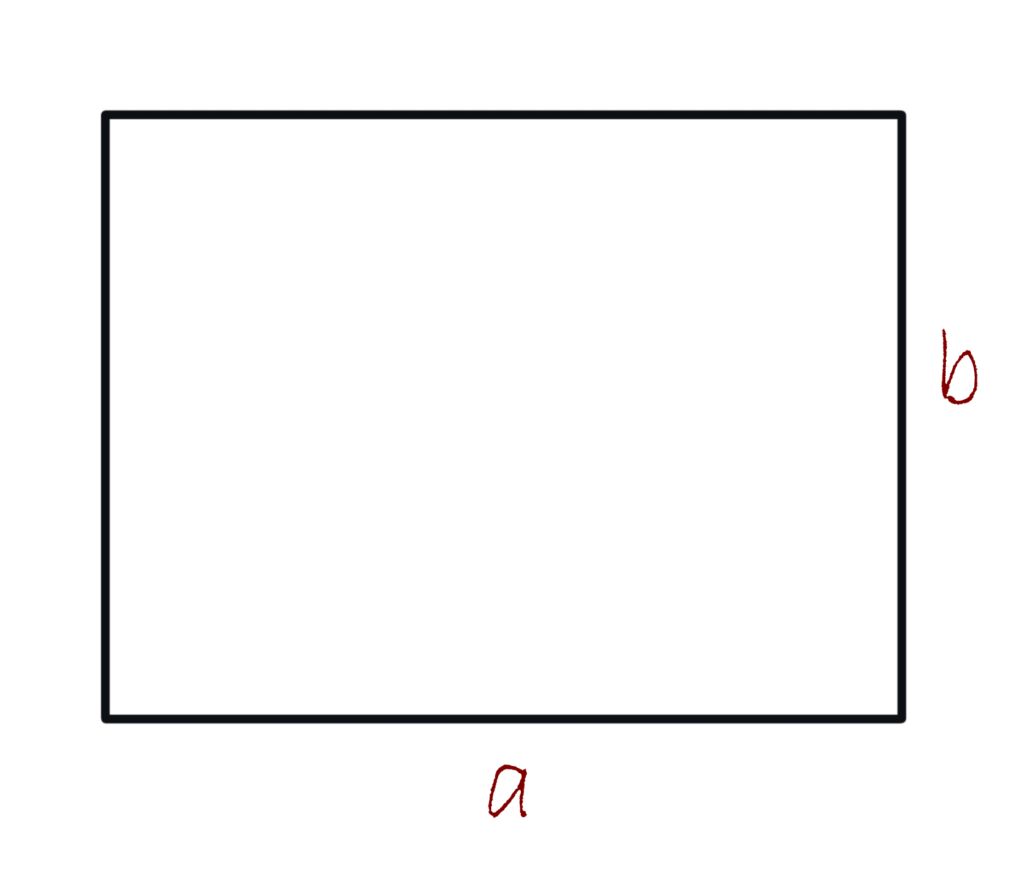
After the algebraic manipulation, it will have a following look:

P=(a+b) \cdot 2

The perimeter of a square

The square is a four-sided polygon with four right angles and four vertices. Each angle is a right angle. All sides have identical lengths, making it easy to calculate the perimeter of a square.

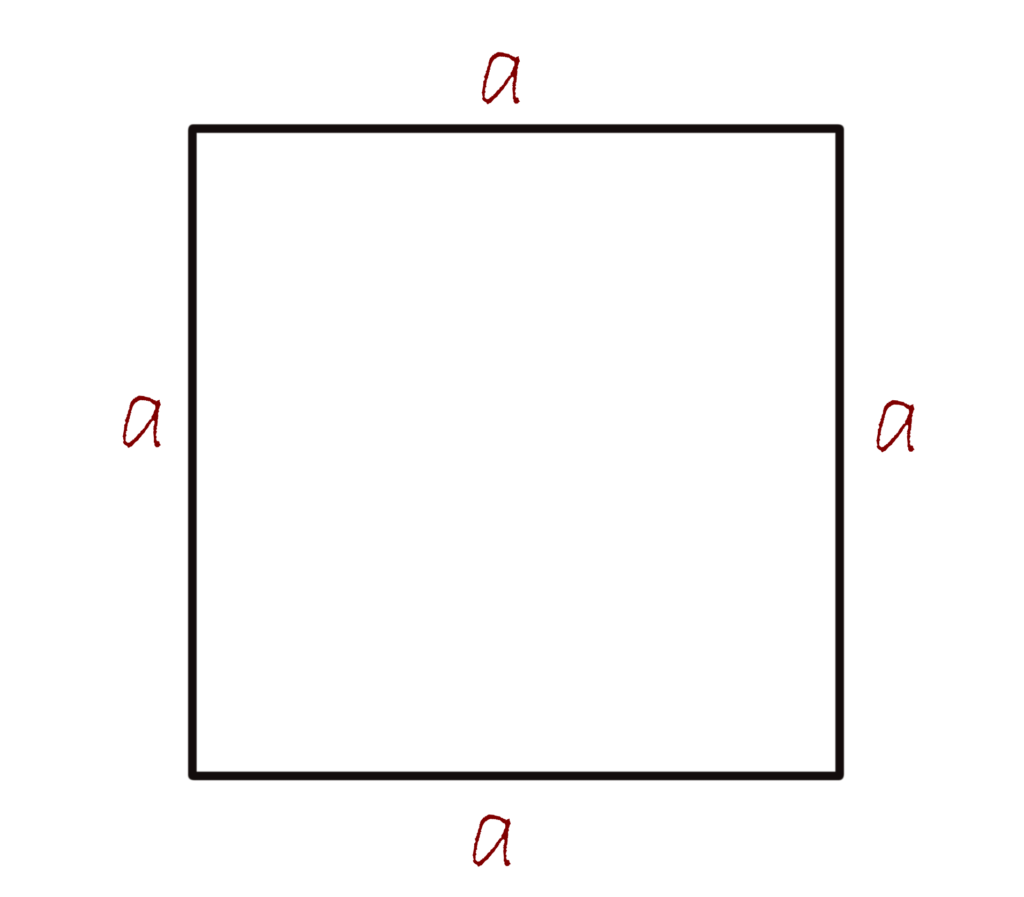
The formula for the perimeter of a square is:

P=a+a+a+a \rightarrow P=4 \cdot a

The perimeter of a triangle

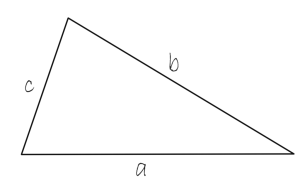
A triangle is a basic geometric shape consisting of three angles whose sum is always 180 degrees. Still, there are different shapes of a triangle, depending upon the value of angles:

An equilateral tringle – all sides equal and each angle is 60 degrees,
An isosceles triangle – two sides of equal length and their angles are also equally measured,
A scalene triangle – all sides have different lengths, and each angle measures differently.

Also, it has three vertices. The formula for the perimeter of a triangle is:

P=a+b+c

The perimeter of a circle

As we mentioned before, the perimeter of a circle is called circumference.

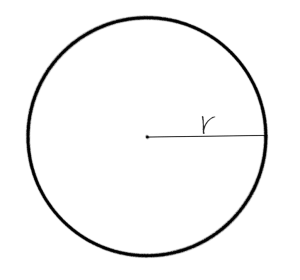
The circumference of a circle is calculated using following formula:

P=2 \cdot r \cdot \Pi

Where the radius of a circle is denoted by r and Π (PI) is the ratio among the circumference and its diameter, and it equals 3.14159265.

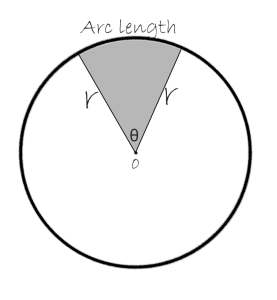
The perimeter of a circle sector

By looking at the image underneath the text, it is easy to notice that the perimeter of a circle sector consists of two radii and an arc length. So the formula for the perimeter of a circle sector is:

P= r + r + Arc \;Length

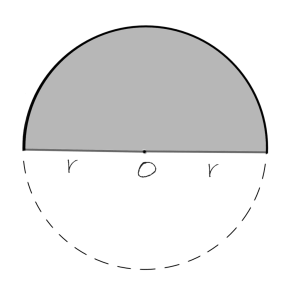
The perimeter of a semicircle

A semicircle is actually a half-circle. This indicates that the formula for the perimeter of a semicircle is half of the perimeter of a full circle plus the length of the line that cuts it half:

P=\Pi \cdot r + 2 \cdot r \rightarrow P=\frac{1}{2} \Pi \cdot d + d

In the previous formula, the radius is denoted by r and diameter by d.

The perimeter of a semicircle — Semicircle

The perimeter of an ellipse

To calculate the perimeter of an ellipse, we need to know the length of the semi-major axis (b) and semi-minor axis (a). Therefore, the approximation formula for the perimeter of an ellipse is:

P= 2\cdot \Pi\cdot \sqrt{\frac{a^{2}+b^{2}}{2}}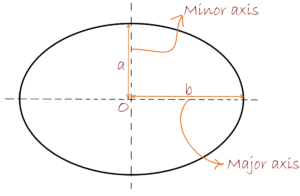

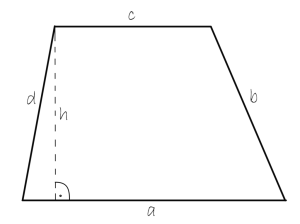
The perimeter of a trapezoid

A trapezoid is a quadrilateral with at least two parallel sides called bases. While the other two are called legs. To find the perimeter of a trapezoid, we need to know the values of bases and legs. The formula for the perimeter of a trapezoid is:

P=a+b+c+d

The perimeter of a trapezoid — Trapezoid

The perimeter of a parallelogram

A parallelogram is a quadrilateral with two sets of parallel sides. Opposite facing parallel sides have the same length. The equation that we use to calculate the perimeter of a parallelogram is:

P=2 \cdot (a+b)

The perimeter of a parallelogram — Parallelogram

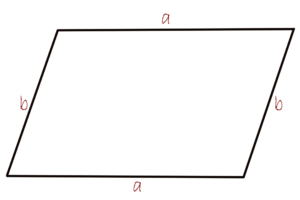
If you want to know more about parallelograms, check out our parallelogram perimeter calculator.

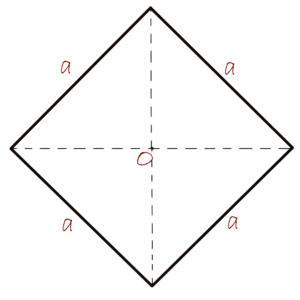
The perimeter of a rhombus

A rhombus is a polygon that is a parallelogram, but a parallelogram is not always a rhombus. Its geometry consists of two sets of parallel sides with the same length, which is the main difference between parallelogram and rhombus. Also, its angles are not necessarily 90 degrees. As we previously stated, a parallelogram does not have all sides of the same length, but it can have. Since a rhombus has four identical sides, the formula for the perimeter of a rhombus is:

P=4\cdot a

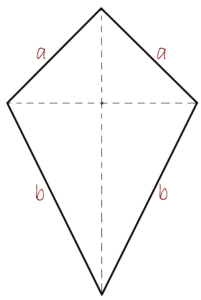
The perimeter of a kite

A kite is a polygon with two pairs of sides of the same length which means it is quadrilateral. In contrast to a parallelogram, whose parallel sides happen to be equal, a kite has adjacent sides equal. Regarding those equal ones, the formula for the perimeter of a kite is:

P= 2 \cdot (a+b)

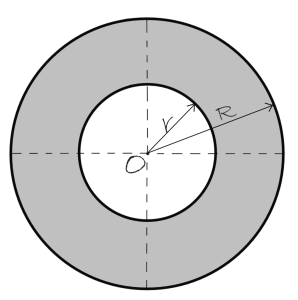
The perimeter of an annulus

An annulus, or the ring, is a two-dimensional circle-shaped figure. On the image underneath the text, you can see that an annulus is the colored part of a circle, and its perimeter is:

P= 2 \cdot \Pi \cdot (R+r)

In the previously written formula, R represents the radius of the bigger circle, while r is the radius of the smaller circle.

The perimeter of polygons with more than four sides

The polygons with more than four sides are pentagon, hexagon, octagon, etc. As we said before, the perimeter is the sum of the length of all sides, and that algorithm stays the same when calculating the perimeter of polygons with more than four sides.

Here are some examples for regular polygons:

Pentagon has five equal sides, which we will mark with a. Therefore, the formula for the perimeter of the regular pentagon is $P=5 \cdot a$
Hexagon has six equal sides, (a) and the formula for the perimeter of the regular hexagon is $P= 6 \cdot a$
Octagon is an eight-sided polygon with equal sides (a), so the perimeter of a regular octagon is $P=8 \cdot a$

When it comes to the regular polygons, we cannot but notice that their perimeter is the product of multiplying the number of their sides with the length of the side. Therefore, in future encounters with the regular polygon, remember to check the number of its sides first. Then measure the length of one side. Afterward, multiply their values, and do not forget to write down the unit alongside the result. Also, a gentle reminder that using our perimeter calculator is way easier.

Perimeter Calculator