Angle Conversion Calculator instantly converts angles from one measurement unit into multiple of them. So regardless of whether you have it in degrees or radians and want to convert into arcmin, arcsec, mil or gon (gradian), including vice-versa scenarios, all of that can be done with the help of this calculator.
Angle Conversion Calculator can be very useful for mathematicians working with geometry or trigonometry daily because it calculates and converts angles quickly and, most importantly, gives you correct results.
If you are interested in calculating the complementary of any angle, besides Angle Conversion Calculator, check out our Complementary Angles Calculator.
What is an angle? – acute, obtuse, right, straight, reflex, and complete
When two rays or lines meet at one point, they form something called an angle in geometry. So the symbol for it is ∠ in geometry, and it depicts its theoretical definition. We see those lines coming from different directions, joining in one particular point.
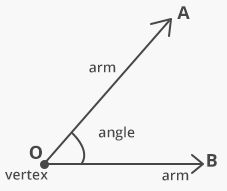
If we mark one line as A and the other with B, they form with the centre point O, an angle ∠ AOB. So, we have different angles depending on how far or close those mentioned lines are. Now, you probably wonder how they are measured and what metrics are used.
In geometry, it is measured and presented in degrees (°) or radians (rad). Thus, we can figure out from the picture above that the farther lines are, the higher the angle they form.
There are some tools that we can use to measure them. The important and most widely used way is with a protractor. When you measure it this way, you need to align the midpoint of a protractor with a vertex point. Then align one side of it with zero line of a protractor and check what the protractor shows.
Parts of an angle
Every angle has two essential parts: vertex (centre) and arms. Vertex is the centre joining point in which arms are met. In the example above, we marked it as a vertex O. However, a vertex is just a straight point in the geometry system without those lines. Therefore, we form a geometric figure, called angle, by combining the vertex with arms (lines).
Each has one vertex and two arms. From the illustration above, we can see that the given has arms: OA and OB.
Types of angles
We saw that the angle value closely relies in terms of the distance between its arms. Therefore, even though a vertex is the centre point, it does not impact its value of it. Having said that, we have a few different types, which I will cover in the following part of the article.
Acute
When the arms are pretty close, they form an acute angle. An acute angle is an angle that is less than 90 degrees.
Right
When the arms are always in the constant distance forming a 90-degree angle, in geometry, we call it a right angle. In addition, it does not matter which of the four possible directions arms are oriented because they always form an angle of 90 degrees.
Obtuse
If the arms are quite distant, forming an angle over 90 degrees but not higher than 180 degrees, we call it an obtuse angle.
Straight
When we see the arms stretched out, forming an angle of constant 180 degrees, geometry defines it as a straight angle.
Reflex
If the arms are overly stretched out, forming an angle higher than 180 degrees and less than 360 degrees, it is considered a reflex angle.
Complete
Complete angles are quite rare in geometry, but they are formed only if the arms of them overlap, making a 360-degree, called a complete angle.
Classification of angles based on rotation direction
Classifying angles by their “openness” is the main classification of them in geometry. However, we can classify them in terms of whether their rotation goes clockwise or anti-clockwise. Based on that, we have two types of them:
- Positive (clockwise rotation, +/+ part of the coordinate plane)
- Negative (anti-clockwise rotation, -/- part of the coordinate plane)
What is a radian, and how to convert degrees to radians?
If we draw a circle and cut its one part by an (arc), the arc length on the circle is considered a radian, or 1 rad. Radian is a math unit used for measuring angles in geometry. You can interchangeably use it with degrees, converting from one to another unit depending on which format you need it to be.
Radians are naturally used in geometry and especially trigonometry, where all the angles are only measured in radians. In addition to that, in many places in physics, you can find radians, such as when we measure angular velocity and acceleration.
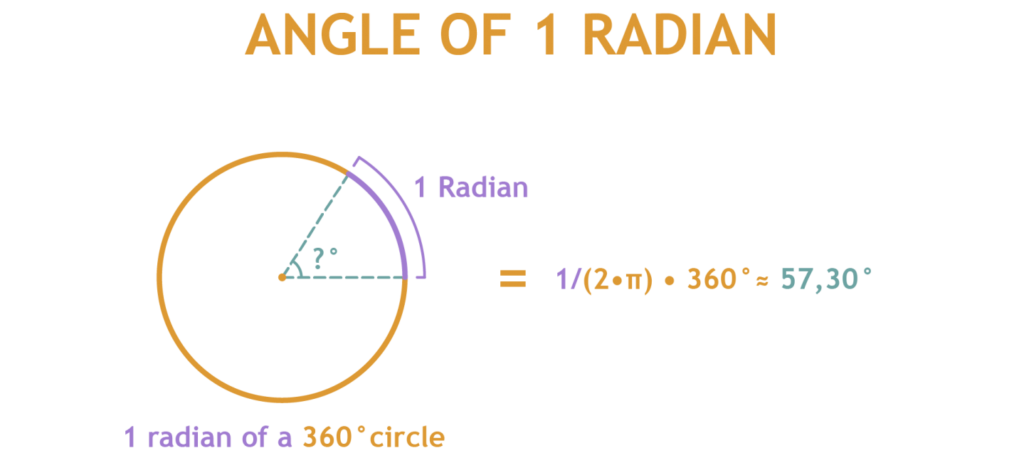
1 Radian is close to 57.2958 Degrees or 2π
Half a circle equals π Radians, while a full circle equals 2π Radians.
Using our Angle Conversion Calculator, let’s find out how conversion works from the unit of degrees to radians.
Steps:
- Open up the converter (calculator)
- Enter an angle that you need to convert from deg to rad in the converter
- The converter will display the result in radians unit (rad)
- Example: 68 deg => 1.19 rad
Note: Our Angle Conversion Calculator supports more measurement units, and you are not limited to only degree-radians conversions. However, we will mention them later.
How to convert degrees minutes seconds to decimal degrees?
Before we step into the conversion part, let’s define what decimal degrees are and where they are used mainly.
Decimal Degrees (DD) is mainly used to express latitude and longitude coordinates in geographic information systems (GIS), such as Google Maps or GPS devices. Decimal Degrees have a fraction of a degree after the decimal point. We use it when we need a high precision of degrees, two, three, or more decimals.
An example of degree minutes seconds (DMS) format:
DMS = 38° 35′ 50″
Don’t worry if you need to do DMS to DD (conversion) because it’s quite easy. Thus, let me take you through the steps:
Step #1:
Since 1 hour has 3600 seconds, we need to divide the number of seconds by 3600.
50 \div 3600 = 0.01388°Step #2:
Convert minutes to degrees by dividing the number of minutes by 60 because 1 hour has 60 minutes.
35 \div 60 = 0.5833°Step #3:
Add these two numbers you got from Step #1 and Step #2.
0.01388° + 0.5833° = 0.59718°Step #4:
Now, add that number to 38°, and you will get Decimal Degrees.
DD = 38° + 0.59718° = 38.59718°Table of Angular Conversions
We mentioned that angles are always expressed in two possible units of measurement, degrees, and radians. However, it does not mean that there are no alternative units, less used, but still, they exist. Therefore, I will show you in the table down below how you can manually convert angles from degrees and radians into other angular units.
Units, symbols and conversion values used in angular conversion to radians
| Unit | Symbol | Convert To | Conversion Rate (Radians) | Conversion Rate (Number) |
| radian | rad | radian | 1 | 1 |
| degree | ° | radian | π/180 | 0.01745329 |
| minutes | ‘ | radian | (π/180)/ 60 | 2.908882 e-04 |
| seconds | “ | radian | (π/180)/ 3600 | 4.848137 e-06 |
| octant | octant | radian | 2π/8 | 0.7853982 |
| sextant | sextant | radian | 2π/6 | 1.047196 |
| quadrant | quadrant | radian | 2π/4 | 1.570796 |
| revolution | r | radian | 2π | 6.283185 |
| gradian | gon | radian | 2π/ 400 | 0.01570796 |
| mil | mil | radian | 2π/ 6400 | 9.817477 e-4 |
Units, symbols and conversion values used in angular conversion to degrees
| Unit | Symbol | Convert To | Conversion Rate (Degrees) | Conversion Rate (Number) |
| radian | rad | degrees | 180/π | 57.29578 |
| degree | ° | degrees | 1 | 1 |
| minutes | ‘ | degrees | 1/60 | 0.016667 |
| seconds | “ | degrees | 1/ 3600 | 2.777778 e-4 |
| octant | octant | degrees | 360/8 | 45 |
| sextant | sextant | degrees | 360/6 | 60 |
| quadrant | quadrant | degrees | 360/4 | 90 |
| revolution | r | degrees | 360/1 | 360 |
| gradian | gon | degrees | 360/ 400 | 0.9 |
| mil | mil | degrees | 360/ 6400 | 0.05625 |
