This calculator enables the easiest and fastest calculation to the arc length problem, which is very common in geometry through schooling. Simply by downloading the CalCon calculators mobile app, the calculations of the arc length will be provided to you, anytime and anywhere. CalCon has developed many calculators and explained each topic if math is your weak spot.
What is the arc length?
It is possible to calculate the length of any curved line. Our article will be based mainly on calculating the arc length of a circle, but we will also provide you with the solution for calculating the arc length of the curved line. Firstly, let’s define the arc length of a circle. The arc length of a circle is a part of its circumference. It is a distance between any two points drawn onto the perimeter, which are not parallel to the centre point. Because if they are parallel, their distance equals their diameter, and if their angle equals 360 degrees, the arc length will then be equal to the circumference. However, a better insight into this definition is showed in the picture underneath.
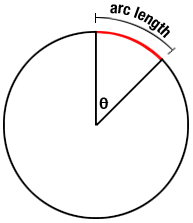
To find an equation for the perimeter of a circle, first, we need to define the relationship between the circumference and diameter of a circle.
\Pi =perimeter/diametar
History of the number Pi
The first document to mention the number \Pi is The Rhind Mathematical Papyrus from 1650 B.C. that estimated this number to be 3.16. More than 1000 years later, the number \Pi was mentioned in the Bible, and its value was estimated to be equal to 3. Later, around 250 BC, Archimedes had an idea of determining the circumference ratio. His method consisted of drawing a polygon inscribed within a circle and circumscribed outside a circle. The more sides of the polygon he drew, the better the calculation was. His approximation of the number \Pi is 3,1418. However, the use of the \Pi was standardised by Leonhard Euler in 1736.
Further analyses by other mathematicians led to discovering more digits that this number contains. The development of computing has given more precise calculations that reach hundreds of decimals for the number \Pi . The value of this number with an adequate number of decimals for our calculations is \Pi = 3.14159.
Arc length-formula
An arc length is directly dependent upon the central angle. Therefore, the formula for the arc length could be calculated in radians and degrees, according to the unit of the central angle. To ease our data manipulation, we will use the following letters to mark the values used in equations:
L- arc length
C-circumference
r-radius
\theta -central angle
A-area of a sector of a circle
To get a formula for an arc length, we will start with the proportion among the arc length and central angle:
\frac{L}{\theta}=\frac{C}{2} \cdot \PiBy inserting C=2*r*pi and doing the algebraic manipulation of the previously given proportion, we get the formula for an arc length:
L=(\theta\cdot \frac{\Pi}{180})\cdot rWe use the equation above when \theta is in degrees.
Arc length formula in radians
This paragraph will show you how to convert degrees into radians and vice versa. Probably, the best way to explain this is by providing you with an example. Also, CalCon calculators provided a converter for this issue.
Converting degrees into radians:
Our conversion will be based on the fact that a full circle contains 360 degrees, which is the equivalent of 2 \cdot \Pi radians. If 360\circ=2 \cdot\Pi , dividing the relation by 2, then 180\circ =\Pi . So, the 1\circ = \frac{180}{\Pi} and by acknowledging this, we got ourselves a basis for conversion. For example, let’s convert 30 degrees into radians:
30\circ\cdot \frac{\Pi}{180}=30\cdot \frac{\Pi}{180}= \frac{1}{6}\cdot \Pi radNow, let’s convert the radians to degrees:
\frac{\Pi}{12} rad=? \frac{\Pi}{12} rad \cdot\frac{180}{\Pi}=\frac{180}{12}=15\circThe formula for an arc length in radians is:
L=\Theta \cdot rArea of the sector of a circle
The area of a circle sector is the amount of space enclosed with two radii and an arc. A sector always emerges from the centre of the circle. A segment of a circle is the area that is bounded by an arc and a chord. To find the area of a circle sector, we will also use the proportions. While knowing that the area of a circle equals Ac=r^{2} \cdot\Pi , the proportion will have the following setup:
\frac{r^{2}\cdot \Pi}{2\cdot \Pi}= \frac{A}{\Theta}After fractional sorting, the formula for the area of the sector of a circle will have the following form:
A=( \frac{\Theta}{360})\cdot r^{2}\cdot \Pi – in degrees
A= \frac{1}{2}\cdot r^{2}\cdot \Theta – in radians
How to find the length of an arc (an example)?
The steps to calculate the length of an arc:
- Measure the radius of your circle or write it down if you already know it.
- Decide whether you will use the formula for calculating the arc length in radians or degrees. According to that, the value of the central angle has to be in the same unit, so make sure that the unit of your angle is paired with the chosen formula.
- Now, input the values into the equation, do the math and get the result.
To gain a better insight into previous steps, we will show how it works on an example.
r=15 cm, Θ=30 degrees
L=(\Theta\cdot \frac{\Pi}{180})\cdot r=(\frac{30\cdot \Pi}{180})\cdot 15=7.85 cmHow to find the sector area (an example)?
To find the sector area, follow these two simple steps:
- Values that must be included in the formula to provide a result for the value of the sector area are the radius and central angle, so make sure to have their dimensions.
- Now, according to the angle unit, pick a formula, and do the calculation.
Finally, an example for the sector area, where we also need the radius and central angle dimensions.
A= \frac{1}{2}\cdot r^{2}\cdot \Theta= \frac{10^{2}}{2} \cdot \frac{\Pi}{2}=78.54 cm^{2}How to find the chord length?
The endpoints of the circle sector are the centre of a circle and two points on its edges. If we connect those two edge points, we create a chord. The difference between a chord and a secant is that a chord does not exceed the outer edges. First, to find chord length, we will connect the endpoints (marked with letters H and D, in the picture underneath) with a straight line. Then we will form a triangle by connecting those points with the centre (O). Now, focusing solely on this triangle and drawing a perpendicular bisector from the centre, we will get two right triangles. And the length of a chord can be determined using Pythagorean theory or using trigonometry functions.
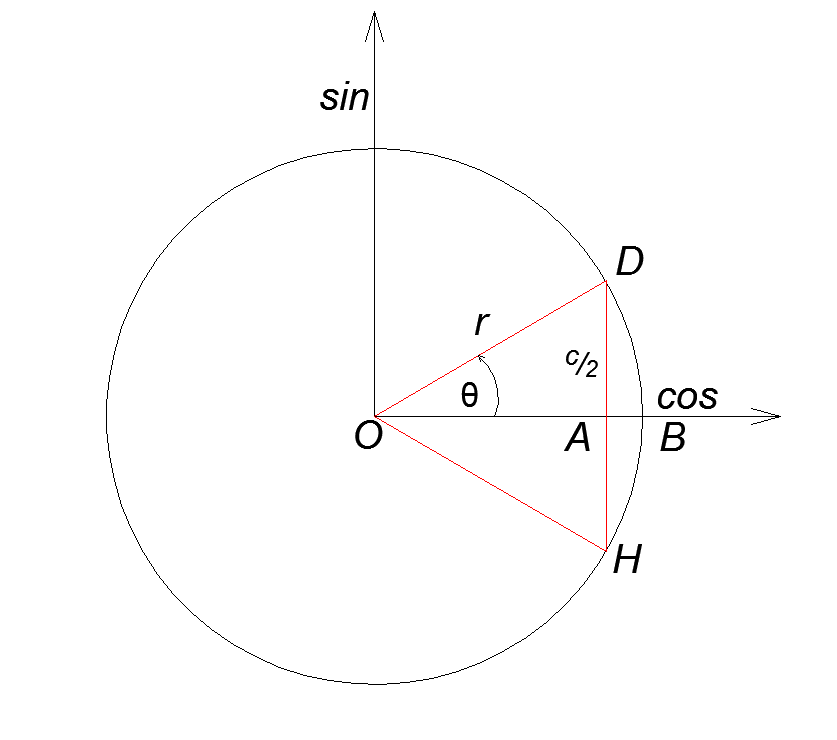
Using Pythagorean theory to calculate the chord length:
r^{2}=b^{2}+(\frac{c}{2})^{2} c=2\cdot\sqrt{r^{2}-b^{2}}Using trigonometry to calculate the chord length:
c=2\cdot r\cdot sin\frac{\Theta}{2}How to find the length of any curve?
The length of a curve can be found using the following formula: L=\int_{a}^{b} ds
where a and b represent x, y, t, or θ-values as appropriate, and ds can be calculated:
1. rectangular form:
ds=\sqrt{1+(\frac{dy}{dx})^{2}} dx ,
ds=\sqrt{1+(\frac{dx}{dy})^{2}} dy2. perimetric form:
ds=\sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2}} dt3. polar form:
ds=\sqrt{r^{2}+(\frac{dr}{d\Theta})^{2}} d\ThetaFAQ
What is the perimeter of an arc?
The perimeter of an arc is equal to the sum of the three sides of the rectangle plus the half-circumference of the semi-circular portion.
How does Arc Length affect cirmumference?
The arc length is a part of the circle’s circumference. For example, an arc with a measure of 30 degrees is one-twelfth of the circle’s circumference, so if we want to find the arc length, it will be one-twelfth of the circle’s circumference.
What do you call the longest chord?
The longest chord is called the diametar of the circle.
What is a central angle of an arc?
A central angle is an angle whose vertex is the centre of a circle and whose sides are radii.
How to find radius with the arc length?
It is possible to calculate the value of the radius if we know the arc length simply by inserting its value into the formula L=(\theta\cdot \frac{\Pi}{180})\cdot r .
How to calculate the arc length by using sector area and central agle?
The first step is to calculate the measurement of the radius by using the formula for the sector area. While knowing the values of the radius and central angle, we can proceed into the formula for the arc length.
