If you’ve ever wondered how to calculate the perimeter of a parallelogram, our parallelogram perimeter calculator will be of great assistance. Not only did we create the most basic equation, but we also implemented two more parallelogram perimeter formulas.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
- Cycloid calculator
What is the perimeter of the parallelogram?
At the same time, the length of the continuous line produced by a parallelogram’s boundary is its perimeter. Also, it has the same unit as its sides. Generally, a quadrilateral is a closed shape formed by the intersection of four line segments. Furthermore, if the opposing sides of a quadrilateral are parallel and of equal length, it is termed a parallelogram. The rhombus, rectangle, and square are all instances of parallelograms. A parallelogram has the following qualities.
- The opposing parties are on an equal footing.
- Angles that are opposite each other are equal.
- Diagonals cut each other in half.
- Each pair of neighbouring angles is supplementary.
However, we may not always be aware of all the sides of a parallelogram. Therefore, we may instead be provided additional information about the parallelogram and asked to calculate its perimeter. In the following examples, the perimeter of a parallelogram may be determined.
- When the positions of two neighbouring sides are known.
- When you know one side and the diagonals.
- When you know the base, height, and any angle.
Parallelogram perimeter formula
In each of these circumstances, below are the formulae for calculating the perimeter of a parallelogram.
- The formula for the Perimeter of a Parallelogram with Sides
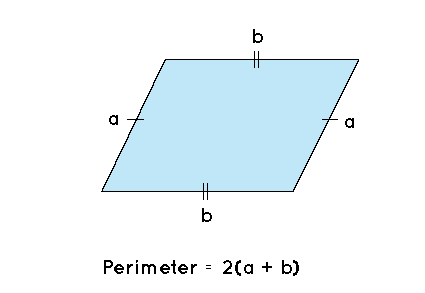
As previously stated, the perimeter of a parallelogram is equal to the total of the lengths of all its sides. Besides, the opposing sides of a parallelogram are equal, as we know. Consider a parallelogram with ‘a’ and ‘b’ on two adjacent sides (the other two adjacent sides will be ‘a’ and ‘b’ alone).
perimeter = a + b + a + b = 2 x (a + b)
- Formula for the Perimeter of a Parallelogram with One Side and Diagonals
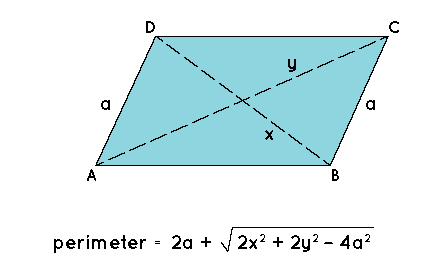
Consider the sides ‘a’ and ‘b’ of a parallelogram with diagonals ‘x’ and ‘y’. Assume that the side ‘ a’ and the diagonals ‘x’ and ‘y’ are all known, but ‘b’ value is unknown, and we’re asked to calculate the parallelogram’s perimeter.
perimeter = 2 x a² + √(2 x e² + 2 x f²- 4 x a²)
The total of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals, according to the converted parallelogram law:
2 x a² + 2 x b² = e² + f²
- Parallelogram Perimeter with Base, Height, and Angle
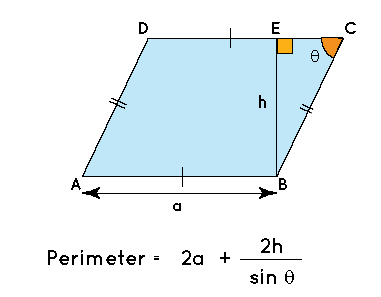
Consider a parallelogram with one of its sides labelled ‘a,’ its matching height labelled ‘h,’ and one of the vertex angles labelled “. Let’s say the unknown side of the parallelogram is ‘b.’ We’ll solve for ‘b’ first, then calculate the perimeter.
perimeter = 2 x (a + (h/sin(angle)))
Because sin(angle) = sin(180° – angle), the neighbouring angles in the parallelogram are supplementary angles. Thus you may select whatever angle you desire.
How to find the perimeter of a parallelogram using this calculator?
Here are a few steps, be sure to follow them to understand 100%:
- Figure out whatever component of the calculator you require. Assume it’s the second instalment.
- In this situation, the values are 15 in, 18 in, and 24 in for the side (a) and two diagonals (e, f). The calculator will notify you if you enter values that do not make a parallelogram. (Think about it: why isn’t creating a parallelogram always possible? Is it feasible to make a triangle of e/2 and f/2 with a=1, e=15, and f=4?)
- The value of the parallelogram perimeter calculator is displayed. It’s a 60:1 ratio.
Calculate the distance AB between (0,0) and (5,10)
The first thing you need to do is input data. We can see that here. For example, we have two points. We will call them points 1 (0,0) and 2 (5,10). Suppose we all know that the values in parentheses represent the x and y variables we represent on the coordinate system as the coordinates of a number. Now that we have defined the coordinates, let’s move on to the more interesting part of this task. Our main task is to find the distance between two given points on a line?
Distance between two points = √(xB−xA)2+(yB−yA)2
= √(5−0)2 + (10−0)2
= √(5)2 + (10)2
= √25 + 100
= √125 = 11.1803
Distance between points (0,0) and (5,10) is 11.1803
Example: The area of the parallelogram ABCD is 54 m2, and its perimeter is 34 m. What are the dimensions of the parallelogram?
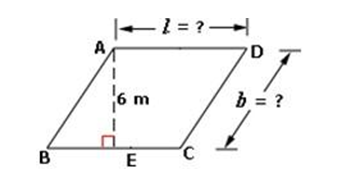
The area of the parallelogram ABCD = base × height = BC × AE = 54 m2 (Given, area of ABCD = 54 m2). Firstly, from the figure above, we can see that the height of the parallelogram is AE = 6 m. The base length of the parallelogram is BC = 54 · AE = 546 = 9 m (Substitute AE = 6.) The perimeter of the parallelogram = AB + BC + AB + BC.
(2 × AB) + (2 × BC) = 34
AB + BC = 17
AB = 17 – 9 = 8 m
