Geometric Mean Calculator

What is geometric mean? – Definition and formula

The geometric mean is a type of average. It indicates the central tendency of a set of values by using the product of the numbers in the set. To calculate it, we need to find the nth root of the product. n is the number of values inside the set. To put it mathematically:

GM_n = \sqrt [n]{n_1 \cdot n_2 \cdot ... \cdot n_n}

To better understand the geometric mean, we need to know what a geometric sequence is. A geometric sequence, or a geometric progression is a specific set of numbers, where every number after the first one, can be calculated by multiplying the previous one by a non-zero number, called the common ratio. Let me give you an example:

2, 6, 18, 54, 162, 486

This is a geometric sequence because every number after the first one (2), can be calculated by multiplying the previous one with the common ratio. In this case, the common ratio is 3, which we can easily prove:

6=2 \cdot \green {3} \\ 18= 6 \cdot \green {3} \\ 54= 18 \cdot \green {3} \\ 162= 54 \cdot \green {3} \\486=162 \cdot \green {3}

Now, if we wanted to find the geometric mean of two numbers in this sequence, we simply take the number that is in-between those two in the sequence. So, if you wanted to find the geometric mean of 54 and 486, you would take the number in-between those two:

2, 6, 18, \blue {54}, \red {162}, \blue {486}

And if you want to double check:

GM = \sqrt {54 \cdot 486} = \sqrt {26244} = 162

You can repeat this with any two numbers in the sequence, and everything will check out.

It applies only to positive numbers, since in order to get roots of negative numbers, we would have to use imaginary numbers. We use it for calculating things that are exponential in their nature, or are meant to be multiplied together. Because of this, it is often used in investing.

How to calculate the geometric mean

To bring this closer to you, let’s do an example.

Let’s say that, in 2018, you bought stocks for $1000. In 2019, the price of the stocks rose 10%. The following year, they rose another 13%, and the year after that, they rose 15%.

\text {Year 1:} \enspace \boxed {\$ 1000} \\ \text {Year 2:} \enspace \$1000 \cdot 1.1 = \boxed {\$1100} \\ \text {Year 3:} \enspace \$1100 \cdot 1.13 = \boxed {\$1243} \\ \text {Year 4:} \enspace \$1243 \cdot 1.15 = \boxed {\$1429.45}

What we have here is another geometric sequence. Now, the question is, what is the absolute rate of return (ABR), and what is the yearly average rate of return (AVR) on the investment. We can easily calculate both of these.

For the absolute rate of return, we need the product of the three multipliers:

ABR = 1.1 \cdot 1.13 \cdot 1.15 = 1.42945

In other words, if you wanted to go from the first year to the last year, you would multiply the initial investment with the absolute rate of return:

\$ 1000 \cdot 1.42945 = \$ 1429.45

The yearly average rate of return would be equal to the geometric mean of the multipliers. Since we already know their product, we can simply calculate the 3rd root of that product to get the yearly average rate of return:

AVR = \sqrt [3] {1.42945} = 1.12647871394

Now, if we take the initial investment, and calculate it by the yearly average rate of return three times, we will get the final value:

\$ 1000 \cdot 1.12647871394 \cdot 1.12647871394 \cdot 1.12647871394 = \$ 1429.45

Use for triangles and other applications in geometry

The geometric mean, unsurprisingly, got its name in geometry. Let me explain.

Let’s say we have a rectangle, whose sides are 2 meters and 8 meters long, respectively. As we know, the surface area of this rectangle is:

S = a \cdot b \rightarrow S = 2m \cdot 8m = 16m^2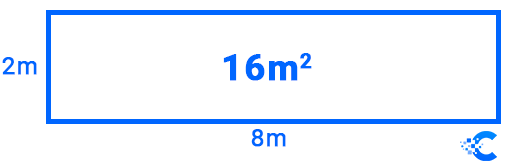

Now, how would we construct a square which has the same surface area as this rectangle. As we know, the formula for calculating the surface area of a square is:

S=a^2

Since we already know the surface area, we can easily calculate a:

16m^2=a^2 \rightarrow a = \sqrt {16m^2} = 4m

What we have calculated here is essentially the geometric mean of the two sides of the rectangle. We multiplied their lengths, and took the square root of the product.

In geometry, the geometric mean theorem states that, in a right triangle, the length of the altitude on the hypotenuse is equal to the geometric mean of the two lines it creates on the hypotenuse. To put it mathematically, if the two lines that were created on the hypotenuse when we drew the altitude were p and q, the length of the altitude h would be:

h=\sqrt [2]{p \cdot q}

Because it was mentioned in book VI of Elements, Euclid is considered the originator of this idea. In that book, he gives an example of how to square a rectangle, which can be done using the geometric mean.

Differences between the arithmetic and the geometric mean

The arithmetic mean is the one we think of when we say average. The formula for calculating it is:

AM = \frac {x_1+x_2+...+x_n}{n}

However, as we know, there are many types of means. The main difference between these two, that you need to keep in mind, are their uses. While the arithmetic mean is the one that is most often used, sometimes it can give you the wrong picture.

We use the arithmetic mean when calculating the central tendency of a set of absolute values. But even then, if the set has great outliers, we get something known as skewed distribution. For more information about the arithmetic mean, you can check out our Mean Calculator!

FAQ