Supplementary Angles Calculator shows whether two angles are supplementary or not. Also, if you input the value of an angle, it shows its supplementary angle’s value. The CalCon team developed a tool that does all the work with supplementary angles for you.
Don’t miss these related posts such as Clock Angle Calculator, or Perimeter of a Triangle, and many more. Also, you will learn about trigonometric functions and their use in geometry, 45 45 90 triangle calculator, 30 60 90 triangle calculator.
Make sure to take your time to investigate the content on our site. Also, let us know if there is a specific topic on whom you would like to know more so that we can write about it.
First, let’s learn about some basics in geometry that will help us to understand better the supplementary angles:
- An angle is a part of a plane bounded by two rays with the same endpoint (vertex).
- A plane is a two-dimensional surface with zero thickness, zero curvature, and continuous length and width.
- A degree (° the degree symbol) is a measurement of an angle, and it represents \frac{1}{360} of a circle.
- A radian is SI derived unit of an angle, where one radian is defined as an angle whose vertex is the center of a circle, while the rays expand, creating an arc whose length equals the radius of a circle. A radian is a dimensionless value. However, the symbol rad is used to denote radian.
Take a look other related calculators, such as:
- Phase shift calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is a supplementary angle?
The word supplementary has its roots in Latin as a combination of words, “Supplere” and “Plere.” The meaning of these two words will set the foundation for the definition of supplementary angles. According to the meaning of “Supplere,” which is to supply, and “Plere” means to fill, we get “when something is supplied to complete a thing.” Now let’s gather all the puzzle pieces and form a precise definition.
Two angles combined must have a sum of 180 degrees or \pi radians in order to be supplementary. Check the Angle Conversion post to learn more about conversion between different units. That is, they need to create a straight angle while sharing their common side. Sharing a common side is not always a case. Therefore, angles don’t need to have common sides or vertex to be supplementary. In conclusion, the only request for them to be supplementary is to add up to 180 degrees.
Supplementary angles definition and relationships
As we stated previously, two angles that add up to \pi radians or 180 degrees are supplementary. Only two angles can form a supplementary angle, while they are both right angles or an obtuse and acute angle. Math is very simple when it comes to writing down the formula for supplementary angles, which is given below:
\alpha+\beta=180 °
Three geometry theorems mention supplementary angles:
- Congruent Supplements Theorem – If two angles (\angle \alpha and \angle \beta ) are both supplementary to a third angle ( \angle \gamma), then \angle \alpha and \angle \beta are congruent.
- Same Side Interior Angles Theorem – Interior angles made by a transversal intersecting two parallel lines on the same transversal side are supplementary.
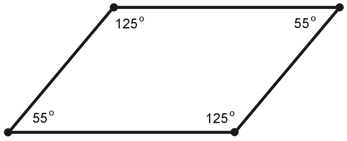
- Consecutive angles in a parallelogram are supplementary – One property of parallelograms is that their consecutive angles are supplementary.
In trigonometry, supplementary angles sines are equal, but their cosines and tangents, unless undefined, are equal in magnitude while having opposite signs. Learn more about it in this Cofunction Calculator post.
The trigonometric connection between supplementary angles:
| sin (180° – θ) = sin θ | sin (180° + θ) = – sin θ |
| cos (180° – θ) = – cos θ | sin (180° + θ) = – sin θ |
| tan (180° – θ) = – tan θ | tan (180° + θ) = tan θ |
| csc (180° – θ) = csc θ | csc (180° + θ) = – csc θ |
| sec (180° – θ) = – sec θ | sec (180° + θ) = – sec θ |
| cot (180° – θ) = – cot θ | cot (180° + θ) = cot θ |
Interestingly, the sum of the angles in a triangle is 180 degrees. Therefore, the sum of any two of its angles is supplementary to the third angle. Also, knowing that a parallelogram has opposite angles of equal measure, it is easy to notice that its adjacent ones are supplementary. Another example of supplementary angles is the opposite of a cyclic quadrilateral.
Supplementary angles proof
Now, we will provide proof for the theorems stated above:
- Congruent supplements theorem:
Since, \angle \alpha + \angle \gamma=180 \degree , and \angle \gamma + \angle \beta=180 \degree , therefore, \angle \alpha and \angle \beta are congruent.
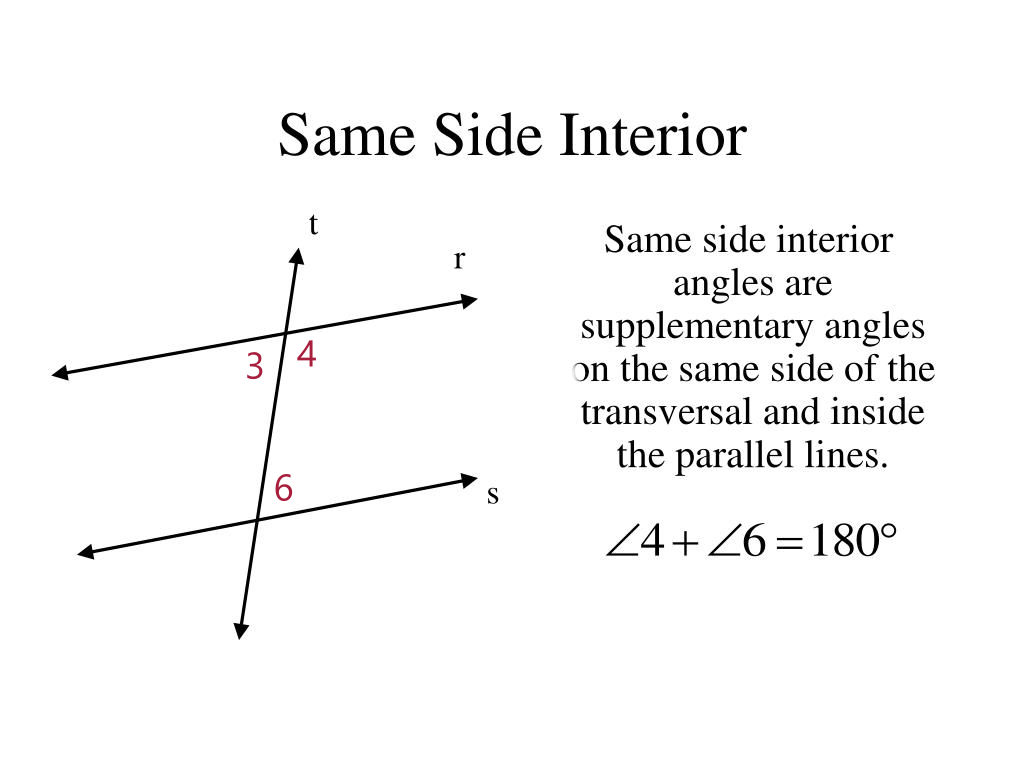
- Same side interior angles theorem:
The proof for this theorem lies in the very definition of supplementary angles, and since \angle 3 and \angle 4 form a linear pair, they are supplementary and by the Alternate Interior Angle Theorem, \angle 3=\angle6. Thus \angle 4+\angle 6=180 \degree , therefore they are supplementary.
- Consecutive angles in a parallelogram are supplementary:
Complementary vs. supplementary angles
Let’s make a comparison of these two types of angles. Firstly, the main difference in the definition is that complementary angles form an angle that measures 90 degrees, and the sum of supplementary angles is 180 degrees. In other words, a complementary angle forms a right angle while a supplementary angle forms a straight angle.
Supplementary angles are also known as linear pairs of angles. That means they are adjacent, and the side they don’t share forms a straight angle. But, we cannot say that the same rule applies to the complementary angles.
Also, both types of these angles are formed of two angles. In the combination of complementary angles, each participating angle complements the other (complement), and when it comes to supplementary angles, each angle supplements the other (supplement).
Adjacent supplementary angles
The term adjacent in geometry, specifically for angles, means that the angles share a common side and vertex. In short, if they don’t match these demands, they are non-adjacent angles. Now that we clarified the difference between adjacent and non-adjacent angles, we can define adjacent supplementary angles as two angles that share a side and vertex, and the sum of their angles is 180 degrees.
Supplementary Angles Calculator – How to use it?
The supplementary angles calculator provided by CalCon calculators is easy to use. In fact, it is so easy to use that it takes only two steps to calculate a result:
- The first step is to choose if you want to know whether two angles are supplementary or which angle is a supplement to the one you have.
- In the second step, If you choose to calculate a supplementary angle, you will have to enter the value of the angle in this tool whose supplement you want to know. And, if you want to check if the angles are supplementary, enter both of their values, and the calculator will provide you with an answer. Pretty simple!
Practical example
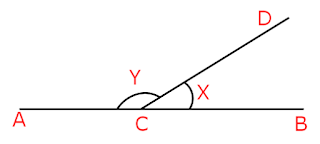
Example 1:
Find angle Y, if angle X=56°.
Example 2:
Find the values of Angle \alpha and Angle \beta , if they are supplementary angles such that \angle \alpha = (2 \cdot x + 10) \degree and Angle \angle \beta = (6 \cdot x − 46) \degree .
Solution:
Since Angle A and Angle B are supplementary, their sum is 180°
\angle \alpha + \angle \beta = 180 \degree (3x + 20) + (4x - 29) = 180 \degree 7x - 9 =180 \degree 7x = 189 \degree x = 27 \degreeTherefore, Angle \alpha = 2\cdot 27 + 10 = 64 \degree and Angle \beta = 6 \cdot 27 - 46 =116 \degree
To sum up, supplementary angles calculator, provided by the CalCon calculator team, is free of charge and helpful, so don’t hesitate to click on the download button and try it out, or you can do the calculation directly on this post, based on the given formula.
FAQ
Supplementary angles in real life?
Examples of supplementary angles in real life are an open laptop placed on the desk, a chandelier hanging on the ceiling, an opened book with a lifted page, etc.
Supplementary angles in a parallelogram?
Adjacent angles of a parallelogram are supplementary.
Are supplementary angles always congruent?
No, they are not always congruent, but they can be. Read more about this in heading – Supplementary angles definition and relationships.
Are vertical angles supplementary?
Vertical angles are supplementary only when they measure 90 degrees.
Can supplementary angles be adjacent angles?
Supplementary angles can be adjacent and also non-adjacent.
