The calculator provides a 360-degree field of view and allows you to calculate the exact angle of the clock relative to the horizon. The result is in degrees and fractions of a degree. For the purpose of calculating clock angle, you can use our clock angle calculator. Without delay, it will help you solve math problems with the clock. How do you find the fastest clockwise angle for a given period? How will the analog clock hands move every hour and every minute? In short, reading this article you will find the answers to these questions and much other necessary information.
What Is the Clock Angle Formula?
The Clock Angle Formula is a math formula that can calculate the angle of a clock face. Generally speaking, with this formula you can find an angle of one hour per hour. The clock consists of three „hands“ for measuring time. These three hands are the hour hand, the minute hand, and the second hand. The watch has 12 divisions of the total 360o angle measure. Using the clock angle formula, you can calculate the time between two hands on the clock.
We have 12 divisions per hour, and the angle between the two divisions is 30o. To sum up, each of these divisions has a division of 5 equal parts, and each element is similar to one minute and has a distance of 6o. Below, you can see what it looks like:
| Minutes | Angular value |
|---|---|
| 1 minute | 6o |
| 2 minutes | 12o |
| 3 minutes | 18o |
| 4 minutes | 24o |
| 5 minutes | 30o |
| 6 minutes | 36o |
| 7 minutes | 42o |
| 8 minutes | 48o |
| 9 minutes | 54o |
| 10 minutes | 60o |
Clock angle problems are related to two different measurements, namely time and angles. The time is based on a 12-hour clock. With this in mind, if you want to solve the problem, you need to observe the rate of change of the angle in degrees per minute. The clock hand of a typical 12-hour analog clock rotates 360 degrees in 12 hours or 720 minutes or 0.5° per minute. The minute hand rotates 360° in 60 minutes or 6° per minute.
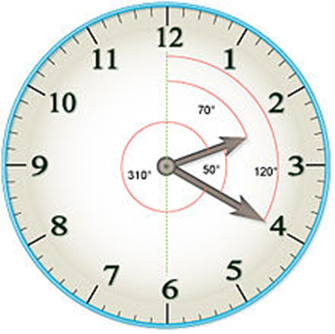
Clock angles – the angle between clock hands
In a word, this calculator will help you find out the angle between the clock’s hands. In a moment, you will measure the angles, and it will show you the exact time.
Looking at an analog clock, you can see that a shorter clock hand can make a full turn in 12 hours. That tells you to move 30 degrees every hour. So, it looks like this:
\frac{360}{12} = 30The clock hand moves half a degree every minute, and it looks like this:
\frac{30}{60} = 0.5In fact, the minute hand moves 6 degrees every minute. This tells you that it rotates entirely in 60 minutes.
\frac{360}{60} = 6With the use of our calculator, you can quickly come up with a solution, either logically or with the help of a formula. Therefore, you will easily find the angles that create the hands of the clock.
How to find the angle between clock hands
Sooner or later, you will wonder what the angle between the hands of a clock is? If you are trying to find the angle between two clock hands, you need to measure the distance between the two hands. Firstly, you will need to know the time on the clock. In a few steps, we will show you how you will get the results:
- As soon as you know the time, you will need to subtract 12 hours from it.
- Next, you will need to subtract the number of hours from the time on the clock.
- Then, you will need to subtract minutes from the time on the clock.
- Finally, divide the minutes by 60. It will give you the angle between the clock hands.
A simple clock math problem: Example and solution
The angle between the clock and the minute is simple when the clock is complete. The minute hand is at number 12, so the angle is equal to the clock multiplied by 30 degrees.
Here is an example. It is 5:00. What angle is between the hour and minute hand on a clock?
As can be seen in an example, the analog clock shows 5 o’clock and this represents the angle between the hands of the clock:
30\cdot 5 = 150In this case, the result is 150 degrees. In the first place, there are two angles between the analog clock. The first is the one we calculated, and the second represents the space on the other side of the hour and minute hand.
360 - 120 = 240It is important to realize that with the use of a calculator, you can get two corners sewn clockwise:
- Angle from the hour hand to minute – 240 degrees,
- Angle from minute to clockwise – 120 degrees.
Find the clockwise angle between the minute hand and the hour hand at 13:55 PM
This clock face is equipped with an hour hand, a minute hand, and a second hand. It is an analog clock, and in the first place, it displays the time as a series of 12 numbers. At 13:55, the minute hand is pointing at 55, and the hour hand is pointing at 13.
Indeed, you can find the angle between the minute hand and the hour hand by subtracting the angle of the minute hand from the angle of the hour hand. The angle between the minute hand and the hour hand at 13:55 PM is a difference of 30 degrees.
If a clock shows 3:00 PM, what is the measure of the angle made between an hour hand and a minute hand?
The watch has a 360 degrees angle in the middle, and the watch is divided into 12 parts. These 12 parts represent a complete 360 degrees angle. So, 1 unit represents as:
\frac{360}{12} = 30To clarify, our task is to find the angle between the hour and minute hands at 3:00 PM. The number of units between the hour and minute hands at 3:00 PM is 3. You calculate the angle as follows:
3 \cdot 30 = 90So, we can say that our solution is at a 90° angle.
FAQ?
1. How do you find the angle of a clock?
There are several ways to express the angle of the clock. Firstly, you can measure the angle of the clock using a protractor. You can also use our calculator to calculate the angle of the clock. An equally important way to find the angle of the clock is to find the time on the clock. After all, you can measure the distance from the center of the clock to the 12 o’clock position. Finally, you can measure the distance from the center of the clock to the top of the clock.
2. What is the angle between the hour hand and minute hand calculator?
The hands-on clock is set at the same angle so you can use it to calculate the angle between the hour hand and the minute hand. In addition, the two hands on the clock that you can use to determine the time are the clock hand and the minute hand. The angle calculator between the hour hand and the minute hand measures the time elapsed since the last full hour.
3. What is the angle for 12 o‘clock?
Any hand represents a complete clock cycle. The angle between the clock’s hands at twelve o’clock is zero degrees.
4. What is the formula of the clock?
The right angle (vertical) is an interval of 15 minutes.
It is 22 times in 12 hours or 44 times in 24 hours which is actually one day.
Right angle (Straight line) or 180 ° = 30 minutes interval.
Right angle = 11 times in 12 hours or 22 times in 24 hours which is actually one day
With the help of our calculator, you can easily calculate the angle from the hour to the minute and vice versa. You need to enter the number of hours and minutes for which you want to calculate the angle.
