Complementary Angles Calculator

You are in the right place if you are interested in calculating the complementary angle to a given angle. You can very quickly check the complementarity of angles, learn more about the meaning of the term complementary angle and how our new CalCon calculator works. Read and learn more about all of this below in the article.

What is the definition of complementary angles?

The meaning of the word complementary comes from two words of Latin origin, namely “complere“ and “plere“. The word “complere” means something complete, while the word “plere” means “fill”. Therefore, the literal translation and the meaning complementary refer to something completed to perfection. The complementarity procedure mainly refers to angles, a pair of angles that add up their values to form an angle of 90 degrees.

You can imagine this as two puzzles. When you connect them, fill the space between the gaps and create a new angle of 90 degrees. Remember that it is always a pair of angles that complement each other. There is no case of complementarity between three or more angles. Each angle must be acute, and its value must be less than 90 degrees.

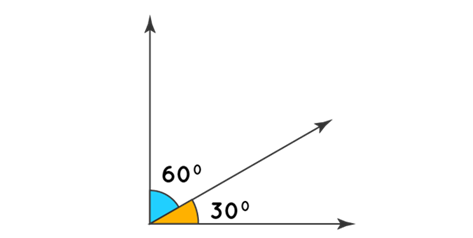
How to find complementary angles?

For the procedure of calculating and finding out whether the angles are complementary, you need to know that the sum of the values should be equal to 90 degrees. The formula to help you calculate looks like this:

Complementary angle = 90 degrees – the value of the angle

If the sum of the angles is equal to 90 degrees, the angles are complementary. Otherwise, there is no proof of the complementarity of the angles.

If this procedure is too complex for you, you can use our phenomenal calculator to take advantage of faster calculations. The calculator works on the principle that you enter the angle value in the provided empty field (whose value must be less than 90 degrees). Within a few seconds, the calculator will throw out its complementary angle.

For example, you have a known value of an angle of 44 degrees, and you need to find its complementary angle. By entering the data into our calculator, based on the calculation and subtraction of the value of 90 degrees, the complementary angle of the angle of 44 degrees is 46 degrees.

Non-adjacent and adjacent complementary angles

You need to distinguish two complementary angles in geometry known as adjacent and non-adjacent complementary angles. In the case of complementary angles, these are angles with a common tip and side. The sum of which gives a new angle that has a value of 90 degrees. In the image below, you can see one example of two adjacent complementary angles:

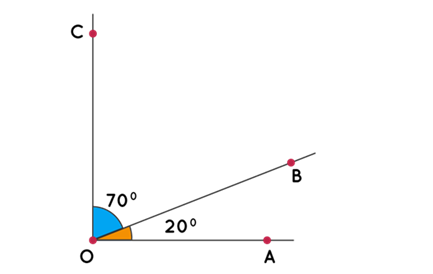
Otherwise, two non-adjacent complementary angles do not have a common tip and thus do not come into contact with any of the sides or vertices of the given angles. Just as it was for adjacent complementary angles, it is also true for non-adjacent complementary angles. The sum must be equal to 90 degrees too. Below you can see an example of this type of complementary angle:

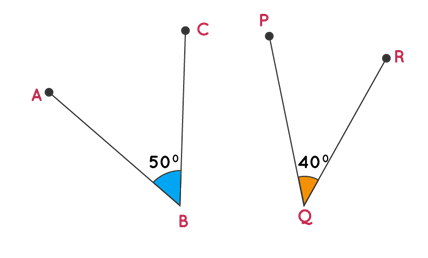
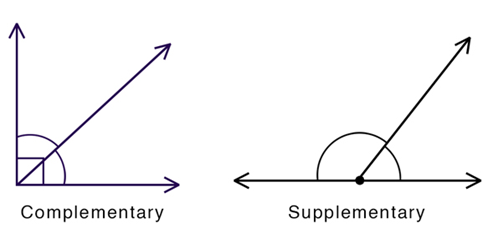
Complementary and supplementary angles

In addition to the complementary angles, we are also familiar with the so-called supplementary angles. Supplementary angles are angles whose common values form an angle of 180 degrees. To determine the supplementary angles, one of the angles must have a value greater than 90 degrees. So, in the end, their sum gives a new angle of 180 degrees. If you have two 90 degree angles, they are supplementary to each other. If you cannot remember these characteristics, it may be easier to remember that the letter S from the name supplementary can associate you with two supplementary angles forming a “straight” angle. In the case of complementary angles, the letter C is associated with “corner”, because these angles have a standard corner angle.

Complementary angles relations

Since the whole story with angles is related to trigonometry, making your situation even more difficult. If you have two angles α and β, how to know if they are complementary? Just follow the basic formula that says α + β = 90 degrees. According to the rules of trigonometric laws, the following applies:

sin\alpha = cos\left ( 90-\alpha \right ) = cos\beta

cos\alpha = sin\left ( 90-\alpha \right ) = sin\beta

The sine of the angle is equal to the cosine of its complementary angle. When it comes to the tangent of an angle, it is in the reciprocal ratio of the tangent of its complementary angle, which we can represent in this way:

tan\alpha = tan\left ( 90-\beta \right ) = \frac{1}{tan\beta }

The main thing to remember when mastering trigonometric connections between complementary or supplementary angles is that the trigonometric function of an angle is always equal to the cofunction of its complementary angle!

Complementary angles example

Example 1:

Based on the display of angles in the graph below, calculate the value of X if it is known that the angles are complementary.

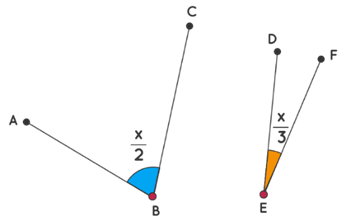
Given the general rule of complementarity of angles, which states that the sum of given angles should be equal to 90 degrees, the following math expression follows:

\frac{x}{2} + \frac{x}{3} = 90 \Rightarrow \frac{5x}{6} = 90 \Rightarrow x = 90\cdot \frac{6}{5} \Rightarrow x = 108

The value of the unknown x is equal to an angle of 108 °.

FAQ?