This Linear Equation Calculator is a tool for finding a solution and graph of a linear function. Often we need to find the solution or the graph of a linear function, and with our calculator it has never been easier, just input two values and get your results.

Find more math calculators, such as one for calculating the trapezoid perimeter, or maybe you want to do some Cross Product for vectors. On the other hand, there is a lot of more interesting subjects on our site where you can learn what is Trigonometry Calculator, 45 45 90 triangle calculator, 30 60 90 triangle calculator for example, or check out PSI to GPM Calculator as well.

Take a look other related calculators, such as:

What is a linear equation?

In mathematics, an equation is a statement that demonstrates the equality of two expressions. These two expressions are separated only by an equals sign (=). They can consist of any number of values and operations, with the only requirement being the expressions have to be equal.

We usually say an equation has two sides: the right-hand side, and the left-hand side. The right-hand side is generally assumed to be 0. However, this doesn’t always have to be true (we will see some examples later).

Equations are made up of three parts. Those parts are:

  • The constants
  • The coefficients
  • The variables

The given numbers that stand alone are called the constants. They are called that because they don’t change. This means that in any version of a certain equation, they always remain the same.

The coefficients stand with the variables, and they serve to amplify them.

The variables are the unknowns of an equation, the missing parts if you will.

Sir William Rowan Hamilton invented the linear equation in 1843. They are a part of linear algebra, which is a very important branch, not just in mathematics, but other sciences, such as engineering, computing, and many more. The standard formula for one-variable linear equations is:

\underbrace{a}_{\text{{\color{Green}coefficient}}} \cdot \underbrace{x}_{\text{{\color{Red}unkown}}} + \underbrace{b}_{\text{{\color{Blue}constant}}} = 0

5 \cdot x^2 + 2 = 10

This equation would now be classified as a quadratic equation. If you wish to learn more about those, you can check out our quadratic equation calculator.

They can also come in two-variable forms:

{\color{Green}a} \cdot {\color{Red}x} + {\color{Green}b} \cdot {\color{Red}y} + {\color{Blue}c} = 0

Linear equation formula and step by step solution

Solving a linear equation means finding the value of x that makes the equality of the two expressions true. When it comes to the one-variable forms, there is a very simple formula for calculating x:

\large \fcolorbox{Red}{Cyan}{$x = - \frac {b}{a}$}

Let’s do a quick example:

5 \cdot x + 10 = 0 \\ \boxed {{\color{Red}x} = - \frac {10}{5} = {\color{Red}-2}} \\ 5 \cdot {\color{Red}-2} + 10 = 0

This is if we assume a is not 0. If a is 0, there are two possible outcomes. In the case that b is also 0, x can be any number, and the equality will be true. If b is not 0 however, there is no solution to the equation, and it is dubbed inconsistent.

With this formula, you can even use a standard algebra calculator to solve the equation.

How to use the linear equation calculator

Our calculator is pretty simple and easy-to-use. You can use it to solve every one-variable linear equation. All you have to do is enter the coefficient and the constant, and our tool will calculate the unknown. Let’s use the example from before:

5 \cdot x + 10 = 0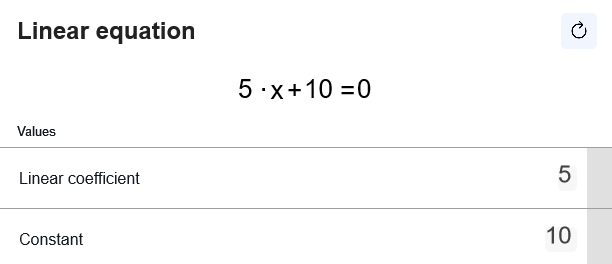

linear equation calculation example 1

And the calculator would get:

linear equation calculation example 2

But what if the equation you have doesn’t have 0 as the end result? Well, there is a simple solution for that too. All you have to do is transfer the result to the left side of the equation, and 0 will be left on the right side. Let’s do a quick example:

10x+10=5

10x+10-5=0\\ 10x+5=0

Don’t forget, when it comes to math, practice makes perfect. Your understanding of this subject will greatly improve if you solve some problems by yourself.

Linear equations with two variables

As we mentioned before, they can also come with multiple variables. For the two-variable ones, the standard form is :

{\color{Green}a} \cdot {\color{Red}x} + {\color{Green}b} \cdot {\color{Red}y} + {\color{Blue}c} = 0

-5x + 4y = 12

As we mentioned, solving any equation means finding the values for the unknowns that make the equality of the two expressions true. When you have two variables, there is more than one solution.

Now, I am going to give you some potential solutions for this problem, and you can try to find the correct one(s).

(4,5) \\ (-4, -2) \\ (4,13) \\ (5,4)

1. -5 \cdot 4 + 4 \cdot 5 = -20 + 20 = 0 ; \boxed {0 \not = 12} ; \text {(4,5) \textcolor{red}{is not} a solution} \\ 2. -5 \cdot -4 + 4 \cdot -2 = 20 + (-8) = 12 ; \boxed {12 = 12} ; \text {(-4,-2) \textcolor{lime}{is} a solution} \\ 3. -5 \cdot 4 + 4 \cdot 13 = -20 + 32 = 12 ; \boxed {12 = 12}; \text {(4,13) \textcolor{lime}{is} a solution} \\ 4. -5 \cdot 5 + 4 \cdot 4 = -25 + 16 = -9 ; \boxed {-9 \not = 12} ; \text {(5,4) \textcolor{red}{is not} a solution} \\

Examples

As we saw in the previous examples, they can gain different forms in certain situations. Essentially, if any value is 0, that part can be left out of the equation. Let’s see some examples.

0x + 5y + 2 = 0

0 + 5y + 2 = 0 \\ 5y + 2 = 0

I mentioned the two basic forms, but there are many more . For example, the slope-intercept form:

y = mx + y_0

Linear function

Linear equations are connected to linear functions. They can come in many forms, but the most common one is the slope-intercept form. As we mentioned, the general formula for it is

f (x) ={\color{Teal}y}= a \cdot {\color{Green}x} + b

{\color{Teal}y} = 2 \cdot {\color{Green}x} + 2

\boxed {{\color{Teal}2} = 2×{\color{Green}0} + 2} \\ \boxed {{\color{Teal}4} = 2×{\color{Green}1} + 2} \\ \boxed {{\color{Teal}6} = 2×{\color{Green}2} + 2} \\ \boxed {{\color{Teal}8} = 2×{\color{Green}3} + 2} \\ \boxed {{\color{Teal}10} = 2×{\color{Green}4} + 2}

Furthermore, if you put this into a graph you will see a vertical line. The vertical line will go through every x and y coordinate (x:1, y:4; x:2, y:6, etc.).

A linear equation in a cartesian plane
A graph of y = 2x + 2

What are systems of linear equations?

A system of linear equations is a set of linear equations that all contain the same variables. A system can have between two and four equations. In order to find the solution for a system, you need to find the values of the unknowns that satisfy every equation in the system. Let me give you an example:

20+10x=0 \\ 8+4x=0

20+10x=0 \\ x = -\frac {20}{10} \\ \boxed {x = -2} \\ 20+10 \cdot (-2)=0 \\ 8+4 \cdot (-2) = 0

These might seem complicated at first, however, the more you practice, the better you will get.

If you are interested in other categories of calculators, you should visit other pages on our site as well. Lots of people are interested in finances, so you can see the posts about rent, such as Net Effective Rent Calculator, or calculate Markdown. Also, you can explore our GDP per Capita page or Perimeter calculator, to see some interesting facts.

FAQ

How to write a linear equation

They come in many forms, but you will most often run into the one-variable (ax+b=0) and two-variable, (ax+by+c=0) linear equations.

How to graph a linear equation 

With our calculator, you can easily graph all your linear equations.