With our Volume of a Rectangular Prism Calculator, you can calculate the volume of a prism with a rectangle as a base. People have always been interested in the mathematical interpretation of our world. Many sciences are built on top of that human will for knowledge. One of the most famous cases is math.
Geometry was especially all the rage in ancient Greece, and the proof is the Pythagorean theorem. In 3D space, this prism is one of the most basic building blocks of all the shapes. That is one of the most basic shapes the human mind can think of, from architecture to everything else.
Furthermore, it’s important to know the volume and area of such a thing. That is because volume is number that represents space something occupies, and area is the measurement of surface.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
- Polygon calculator
Rectangular Prism
Simply put, a rectangular prism (also known as cuboid) is a three-dimensional shape with six rectangular sides. It has three pairs of equal sides. So how does a rectangular prism look? Just imagine a regular box. Here is an image of the shape, with “net” (template of all the faces as a flat surface).
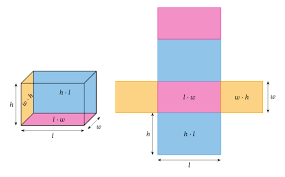
As we see in the image above, opposite sides are equal ones. Technically, cube is also a rectangular prism, but with all equal faces. The rectangular prism has eight vertices and twelve edges.
There is also a definition that rectangular prism has two equal parallel bases, and other sides are parallelograms. We will not explore that case.
Rectangular Prism – Faces, edges and vertices
The term face actually refers to the side of our prism. There are six faces or three pairs of equal faces in this case. All of them are rectangles.
Term edge refers to the line that is the boundary between two faces. A rectangular prism has twelve edges or three quadruplets of equal rectangular prism edges.
Vertex is just a name for the corner on our shape. Our shape has eight rectangular prism vertices. Let’s find out how to calculate the volume of a rectangular prism.
The Volume of a Rectangular Prism – formula
Let’s imagine we put a rectangular prism on the table, so the one whole face is touching the table. Because all the faces are rectangles, which side is down doesn’t matter. So now we can use the formula for calculating the volume of a prism:
Volume = Area\;of\;the\:base \times Height
Our prism has three different edges, width, length, height. If all edges are equal, we are talking about cubes (check out our Volume of a Cube Calculator).
We can calculate the area of the base by multiplying length and width (or using our Area of a Rectangle Calculator). Then, to find the volume of a rectangular prism, multiply the result with the height of your prism. So the formula to find the volume of a rectangular prism is:
Volume\space =Area\;of\;the\:base \times Height = Width \times Length \times Height
With that formula, you can get the volume of any cuboid. Further below, we will explain the usage of our calculator in detail.
Volume of a Rectangular Prism Calculator – How to use it?
When you open our app for the first time, you should see just a regular calculator. Now, you will see the plus sign in the bottom right corner. When you tap plus on that button, the app will lead you to the list of various calculators available in our app.
In the search field on top, enter the Volume of a Rectangular Prism Calculator and tap on the first suggestion. The app will then present you with the interface of our calculator.
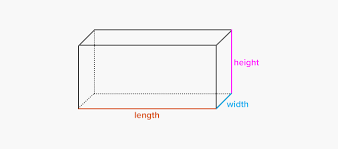
You will see the picture of a rectangular prism with labelled sides on top, so you know which value you are entering. Next, you will see three input fields: “Length (l)“, “Width (w)” and “Height (h)“. You should also see a formula similar to the one we have shown before.
Finally, the field with our result, “Volume“, is the at the bottom. Look closely, and you will see that we can even use different units for our calculations. You can even enter the same length in the three fields, and you will actually get volume of the cube.
If you want, check out our other calculators for calculating surface area, like Area of a Regular Polygon Calculator, and share them with your friends.
Volume of a Rectangular Prism Calculator – example
Rectangular prism shape is so common in math that many rectangular prism examples exist in real world. For example, let’s look at one of the tallest buildings in New York, 432 Park Avenue.
The creator behind this building wanted it to be geometrical, so it’s perfect for our little example from the math standpoint. So, it has the shape of a rectangular prism and dimensions:
Width(w)\space = \space 93.5ft \newline Length(l)\space = \space 93.5ft \newline Height(h)\space = \space 1396ft

If you enter this data into our calculator, you will see that this skyscraper occupies a volume of about 345584 m3.
FAQ
What is the formula for the volume of a rectangular prism?
To calculate the volume of a rectangular prism, you have to multiply the prism’s width, height, and length together. The result is the volume of the prism.
What is a rectangular prism?
A rectangular prism is shape in three dimensions with six faces, all of which are rectangles. Just imagine a shape of a box.
How many edges does a rectangular prism have?
The rectangular prism has 12 edges, of which three are unique. They are called width, height, length.
How many faces does a rectangular prism have?
The rectangular prism has six faces.
