Cube Calculator

Find all the cube elements, the regular mathematical solid, using our Cube Calculator. CalCon offers you a free online tool to calculate all the elements of a cube, such as the diagonal of the cube, the diagonal of one side of the cube, the volume, and the area. In addition to this online math tool, we also offer you an Android and iOS calculators app that you can download for free.

Below you can find the introductory theoretical notes and the definition of the cube, the basic elements of a cube, and a few examples that we will show.

Cube definition

In geometry, a cube is a three-dimensional solid bounded by six square faces, facets, or sides, with three meeting at each vertex.

A cube is a three-dimensional object that has 6 matching squares. The dimensions of all 6 sides of the cube are the same. It is sometimes called a regular hexahedron or square prism. Cube is one of the 5 Platonic solids. It has 6 faces, 12 edges, and 8 vertices. For example, real-life cubes are the ice cube, the Rubik’s Cube, the ordinary cube, and so on.

The shape of a Cube

As mentioned earlier, the cube has 6 faces, 8 vertices, and 12 edges. Each three-dimensional figure has length, width, and height in spatial geometry. Below we will tell basic information about parameters such as the face, vertex, and edge that play an essential role in 3-dimensional objects.

• Faces: The flat area of a 3-dimensional object is known as the face of that object.
• Vertex: In a 3-dimensional object, the point where two or more lines meet is the vertex. Consequently, the angle can be called the vertex.
• Edge: An edge is a segment that connects two vertices.

Below is an example with highlighted parameters.

L = W = H

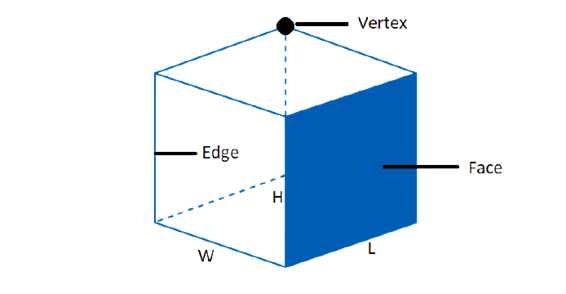
In the figure above, L, W, and H denote the cube’s length, width, and height. Solid geometry is about 3D shapes and shapes, which have surfaces and volumes. In addition we will talk about this below.

Properties of a cube

A cube is considered a special type of square prism because all faces are square and platonic. It has many different properties, just like any other 3D or 2D shape. The properties are as follows:

• The cube has 12 edges, 6 faces, and 8 vertices.
• Cube’s length, width, and height are the same.
• The angles between any two sides are 90°.
• Opposite planes or faces are parallel to each other.
• Opposite edges are parallel to each other.
• Each of the faces meets the other four faces.
• Each of the vertex in the cube meets three faces and three edges.

However, the two most important features of a cube, that we use, are the first two listed above, i.e., it has 12 edges, 6 faces, and 8 vertices, and the that all sides are square.

Cube surface area

There are two types of cube surfaces areas – Lateral Surface Area (LSA) and Total Surface Area (TSA). The LSA is the sum of the areas of all the sides of the cube. For example, the cube has 4 sides, and the sum of its surfaces represents the lateral surface area.

LSA = 4 \times a^{2}

where a is the length of one side.

The Total Surface Area of the cube will be the sum of the area of the base and the area of the vertical areas of the cube. Since all sides of a cube are composed of squares of the same dimensions, the TSA of the cube will be the area of one side five times added to itself. Therefore, it is measured as the “number of square units” (square centimeters, meters, inches, feet, etc.), and you can use our calculator to calculate TSA. Thus, the formula for finding the TSA of a cube is as follows:

TSA = A = 6 \times a^{2}

We will use the TSA below and refer to it as A.

The volume of a cube

Volume is the amount of space in a three-dimensional enclosed area. For all geometric objects, volume is calculated as the base’s product with the object’s height. Volume is often measured numerically using the SI unit, the cubic meter.

The volume of a cube can be calculated based on the length of the side of the cube. There are different formulas based on various parameters to determine the volume of a cube. For example, it can be calculated using the length of a page or the diagonal of a cube and is expressed in cubic units of measurement. As a result, two different formulas for finding the volume of a cube are given below.

The formula for the volume of a cube based on the length of side a is:

V = a \times a \times a = a^{3}

The calculation of the volume of the cube based on the diagonal of the cube is performed according to the following math expression:

V = \tfrac{\sqrt{3} \times d^{3}}{9}

where d is the length of the diagonal of the cube.

Cube diagonals – face and space

Face diagonals are segments of lines that connect opposite corners of the face. Each solid has two, a total of 12 in the cube. The length of the diagonal of a face is calculated based on the use of Pythagoras’ theorem and is given by a formula:

f = \sqrt{2 \times a^{2}} = a \times \sqrt{2}

where a is the length of one side (edge). Since faces are squares, it is the same as the diagonal of a square.

Spatial diagonals are line segments that connect opposite corners of a cube, intersecting its interior. The cube has 4 spatial diagonals. The formula gives the length of the spatial diagonal d:

d = \sqrt{3 \times a^{2}} = a \times \sqrt{3}

How to find the volume of a cube?

The volume of a cube can be easily calculated only based on the length of its edge or the length of the diagonal of the cube, and the formulas are given in the text above.

In essence, it is possible to find any other measure of the cube if we know at least one measure. In this sense, if we know the length of one side of the cube, we can calculate all the other values.

Further, if we know the volume of the cube, we can use it to calculate the length of the side of the cube and then again get all the other values of the cube’s elements, and so on.

However, it is helpful to know some of the following things when it comes to calculating the volume of a cube but also any other element in the cube:

• Volume is a three-dimensional
• We calculate the volume by multiplying the cube’s length, width, and height.
• To calculate the volume of a cube, we need to know and use at least one measure in the cube.
• Volume units are cubic units such as
  • meter m³
  • centimeter cm³
  • inches in³
  • feet ft³

Moreover, it is not bad to know a few basic relations between cubic units. For instance, one cubic centimeter equals 0.061 cubic inches, or one cubic meter equals 35.31 cubic feet.

Cube – an example

We will show a few examples of calculating the basic parameters of a cube. For instance let’s start by having a cube whose side is 6 cm long. Using our calculator, it’s pretty easy to calculate all the dimensions because all you have to do is enter a value in the Side field.

The calculation results are:

• Cube diagonal d = 10.4 cm
• Face diagonal f = 8.49 cm
• Volume V = 216 cm³
• Surface area A = 216 cm²

However, let us take one example of calculating the parameters of a cube if we know the volume of the cube V = 454 m³. Enter this value in the Volume field of our calculator and results are as follows:

a = \sqrt[3]{V} = 7.69 m

d = \sqrt{3} \times \sqrt[3]{V} = 13.31 m

f = \sqrt{2} \times \sqrt[3]{V} = 10.87 m

A = 6 \times V^{2/3} = 354.42 m^{2}

CalCon Cube calculator calculates the cube’s properties by entering any value, and the rest will be calculated automatically, as shown in the text above. Meanwhile, check out our other calculators such as Volume Calculator or Cube Root Calculator.

FAQ

Contact us for any questions regarding this post or other calculators, and anything else we can help you with.