One of the more complex math operations is certainly exponential. Following all the rules related to calculating exponents, the expert team of CalCon company stands behind the creation of a calculator that will make it easier for you when dividing exponents. With our calculator, you can learn more about dividing exponents and the formulas used. We will also explain dividing exponents into different bases and many other exciting things.
And if you are interested in calculating the multiplication of exponents, visit our calculator, but also there is a related Exponential Growth Calculator. Also, head to our other interesting and related calculators such as Segment Addition Postulate, Cofunction, Condense Logarithms or 45 45 90 Triangle calculator. Learn logarithms with this Logarithmic Equation tool, and also learn something about Linear Equation as well.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Sum and difference identities calculator
- Trigonometry calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
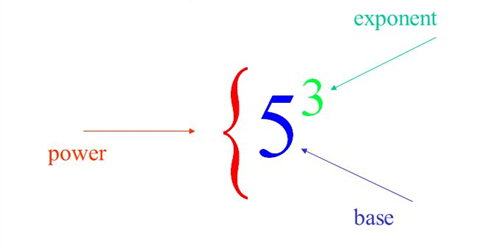
Dividing Exponents: What is an exponent?
In this article, you can find more about the mathematical operation of exponentiation. Accordingly, the notion of exponent needs to be explained. From a linguistic point of view, the term exponent has its origin in the word exponere, a combination of the prefix ex with the meaning to „present“ or „explain“ and proponere, which means “to display.” The newly created word exponere means the one who offers a proposal, which stands for something. From a math point of view, the exponent is the name for the value of how many times the base number will multiply by itself. Essentially unknown x (the base) will multiply with it n (exponent) times.
4^{4} = 4\cdot 4\cdot 4\cdot 4Exponents are also known as indices or power. You can recognize them because, in most cases, they are written in a superscript. With exponents, you can do basic math operations like division and multiplication. In practice, you can also write exponents in the form of positive/negative numbers or the formation of fractions.
How to use the dividing exponents’ calculator? How to use the dividing exponents’ calculator?
After clarifying the preliminary information, it is time to explain how our calculator works. If you are familiar with some of our other calculators in the field of math, you probably understand the ease of use. This calculator contains specific areas that you need to fill in. The required data are the values of the base x and y, and the exponents a and b in the following form:
\frac{x^{a}}{y^{b}}You enter numbers arbitrarily, whether the base is the same and different exponents, or vice versa. Below the blank fields, the calculation procedure after entering the numbers is explained in steps.
How to divide exponents? Dividing exponents rules
Exponential rules have simplified the process of dividing exponents. Here we distinguish two situations that we will explain below, related to the base number. The calculation of the division of the exponents follows the most important rule of the power quotient, which has the following appearance:
\frac{w^{a}}{w^{b}} = w^{a-b}Dividing exponents with different bases
When dividing exponents by different base numbers, you can distinguish two situations, which we will explain with examples below. If you have the bases with different values and the exponents are the same, then you can use the following calculation formula to solve this:
\frac{a^{n}}{b^{n}} = (\frac{a}{b})^{n}In the following example, we will show the use of the previous formula in practice:
\frac{8^{4}}{4^{4}} = (\frac{8}{4})^{4} = 2^{4} = 2\cdot 2\cdot 2\cdot 2 = 16Another situation is that you have both bases and exponents with different values. In this case, it is necessary to calculate each exponent separately and then divide them. You can do this very quickly by following the dividing rule:
\frac{a^{n}}{b^{m}}Here is an example of what it looks like:
\frac{5^{3}}{3^{4}} = \frac{5\cdot 5\cdot 5}{3\cdot 3\cdot 3\cdot 3} = \frac{125}{81} = 1.54Dividing exponents with the same base
To divide exponents with the same base value, you need to use the essential subtraction operation. It would help if you subtracted the different values of the exponents as long as the standard base is the same. By following the following rule of dividing exponents, the calculation process will be much easier for you:
\frac{a^{m}}{a^{n}} = a^{m-n}The following example will help you understand everything we have clarified:
\frac{7^{5}}{7^{3}} = 7^{5-3} = 7^{2} = 49Dividing negative exponents
You have probably encountered the concept of negative numbers and their influence on mathematical operations so far. If not understood in the right way, these are numbers that will lead to problems when calculating them in different mathematical expressions. You need to know the essential information that each negative number has a value less than zero, and you can quickly identify them by a negative sign. The following number line shows some of the values of negative numbers for easy recognition:

If you want to add negative numbers, you need to go left on the number line. Otherwise, by moving to the right then you add the negative number. When multiplying a negative number by a positive one and vice versa, the result will be negative. On the other hand, multiplying two negative numbers or two positive numbers gives a positive result. Each negative number can also be expressed in the form of a fraction, i.e., in the form of their positive reciprocal value as below:
5^{-3} = \frac{1}{5^{3}}The higher the value of the negative exponent, the smaller the number it represents. In translation, a value of 2-3 is more significant than a value of 2-7.
Now, when you know some of the basics of negative numbers, let’s clarify the process of dividing negative exponents. The process is almost the same as the multiplication of negative exponents, and we distinguish several situations, which we will explain with the help of several examples.
Example 1
The first case refers to a situation where you have the same base and different negative exponents, where you follow the rule below:
\frac{a^{-n}}{a^{-m}} = a^{-n-(-m)} = a^{m-n}Example:
\frac{3^{-4}}{3^{-6}} = 3^{-4-(-6)} = 3^{6-4} = 3^{2} = 9Example 2
The second case is defined to have bases with different values while the exponents are the same. In this case, you need to perform a base value divide operation, following the rule below:
\frac{a^{-n}}{b^{-n}} = (\frac{a}{b})^{-n} = \frac{1}{(\frac{a}{b})^{n}} = (\frac{b}{a})^{n}Example:
\frac{4^{-2}}{5^{-2}} = (\frac{4}{5})^{-2} = \frac{1}{(\frac{4}{5})^{2}} = (\frac{5}{4})^{2} = 1.25^{2} = 1.5625Example 3
The third and last case of calculating division with negative exponents is when the values of both the base and the exponent are different. Then we follow this rule:
\frac{a^{-n}}{b^{-m}} = \frac{b^{m}}{a^{n}}Example:
\frac{5^{-3}}{8^{-2}} = \frac{8^{2}}{5^{3}} = \frac{64}{125} = 0.512