You may use this exponential growth calculator to calculate a wide range of operations. First, note that the exponential growth rate, r, can be any positive value; however, we can use this calculator as an exponential decay calculator, with r representing the decay rate, which should be between 0 and 100%. The rationale for this is that a decrease of more than 100 percent compared to the starting quantity would result in a negative value.
What is exponential growth – definition exponential growth?
The curve of an exponential function is formed by a pattern of data that exhibits larger rises with time. Compound returns in finance lead to exponential development. Compounding is one of the most powerful factors in the financial world. This approach enables investors to generate big quantities of money with a small initial investment. Exponential growth is commonly seen in savings accounts with a compound interest rate.
How to calculate exponential growth?
Consider the following scenario: a small city with a population of 10,000 people at the start of 2019 had 10,000 people. It was discovered that the city’s population continues to rise at a consistent pace of 5% every year. What should you do to figure out the population size projections for 2030? We may deduce from the data that the starting population value, x0, is 10,000. In addition, we have a growth rate of r = 5%.
10,000 * (1 + 0.05)t = 10,000 * 1.05t x(t) = 10,000 * (1 + 0.05)t = 10,000 * 1.05t
The number t represents the number of years that have transpired since 2019. In our situation, we shoulduse t = 11 for the year 2030, as this is the difference in the number of years between 2030 and the starting year 2019. Finally, x(11) = 10,000 * 1.0511 = 17,103 is obtained.
As a result, the population of our tiny city in 2030 is expected to be about 17,103.
Exponential growth formula
A quantity that grows exponentially is described as an exponential function of time. The variable denoting time is the exponent (in contrast to other types of growth, such as quadratic growth).
If the proportionality constant is negative, the amount declines with time and is called exponential decay instead. Because the function values form a geometric progression in a discrete domain of definition with equal intervals, it is also known as geometric growth or geometric decay.
Xt=X_0(1+r)t
Exponential growth graph
The graph shows how exponential growth (green) outperforms linear and cubic growth (red and blue, respectively).
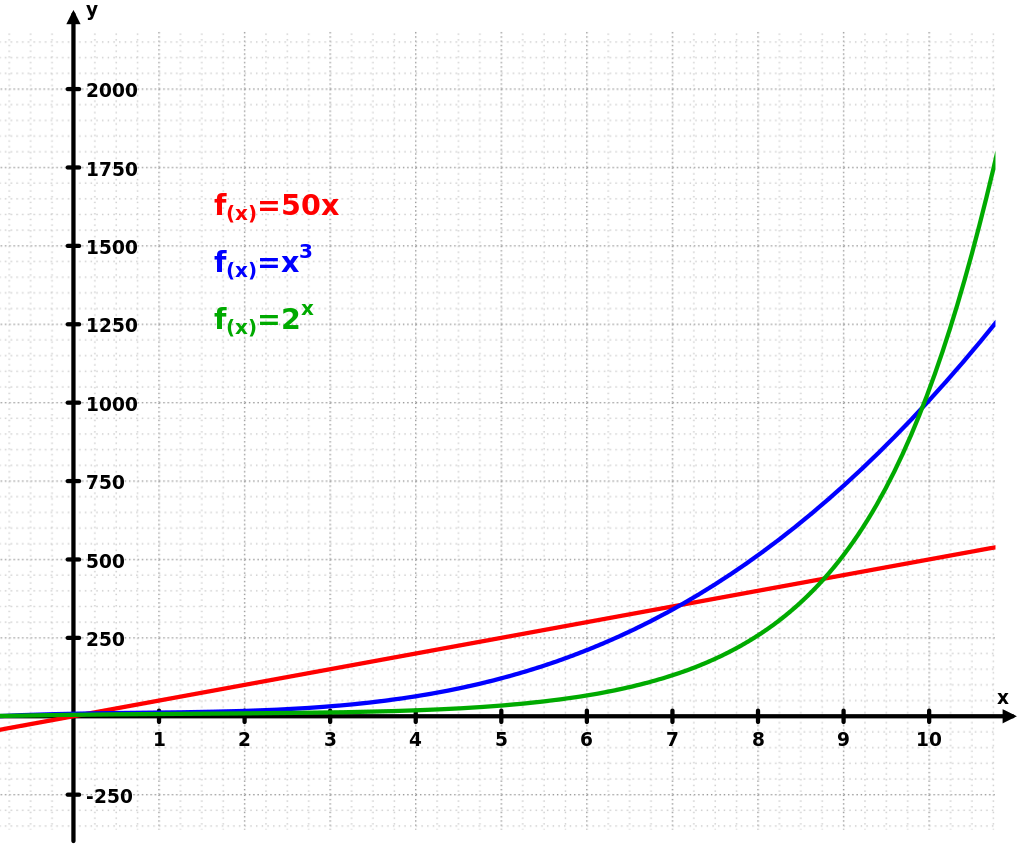
Exponential growth example
Assume you put $1,000 in a savings account that pays a guaranteed 10% interest rate. You will earn $100 each year if the account has a basic interest rate. As long as no further deposits are made, the interest paid will not change.
However, if the account has a compound interest rate, you will receive interest on the whole balance of the account. Every year, the lender will apply the interest rate to the whole amount of the initial deposit, plus any previously paid interest. The interest earned in the first year is still 10%, or $100. However, in the second year, the 10% rate is applied to the increased $1,100, resulting in $110. The amount of interest paid increases each year, resulting in fast accelerated, or exponential, growth. Your account would be valued at $17,449.40 after 30 years if no more deposits were necessary.
Exponential growth vs. decay
Decay occurs when numbers decline exponentially over time, resulting in a result that resembles repeated division. Although an exponential equation is used, the exponent is set to decrease or decay with time.
In exponential growth, the value of numbers grows exponentially over time. But in decay, the value of numbers decreases exponentially over time. In the case of exponential growth, the exponent in the equation is generally an integer, a number larger than one. In the decay equation, the exponent is a fraction between 0 and 1. The y-values on a graph will rise as the x-values increase in exponential growth. The y-values on the graph will drop as the x-values grow in decay.
Linear vs. exponential growth
Linear growth occurs constantly, but exponential growth accelerates over time.
A linear function f(x)=x , has a derivative of f’(x)=1, indicating that it grows at a constant pace. The growth rate will always be 1 – no exceptions – regardless of how long the item or population has grown or how large it has become.
An exponential function g(x)=ex , on the other hand, has a derivative of g’(x)=ex . This means that when the graph becomes larger, the derivative grows with it, making the graph steeper and the growth rate quicker. In reality, the rate of expansion will never slow down.
The continuous exponential growth model
Change is unavoidable as a result of ongoing progress. We can’t point to an incident and say, “This is where it changed.” The pattern always changes (radioactive decay, a bacteria colony, or perfectly compounded interest).
Can time be negative?
You may have noted that exponential growth and decay naturally consider time as just a positive number, implying that we are projecting a future quantity. However, this does not preclude us from applying this formula with negative time values. This means that we characterize the phenomena of interest before the initial observation.
In the case of population growth, you could wonder: what was the population of our tiny city in the year 2000, assuming a constant population growth rate of 5%?
To solve this, you would use t = -19 because the year 2000 is 19 years before 2019. Thus, the solution would be
x(-19) = 10,000 * 1.05-19 = 3.957
Real-world applications of the formula for exponential growth and decay
There are multiple instances when the exponential growth and decay formula is utilized to describe various real-world phenomena:
- Bacterial, viral, plant, animal, and human populations increase
- radioactive decay, drug blood content,
- atmospheric pressure at a specific height,
- compound interest, and economic growth
- radiocarbon dating
- computer processing power, and so forth.
FAQ
What is exponential growth in math?
Exponential growth is the process through which quantity rises over time.
What is the difference between exponential and logistic growth?
Exponential population growth: When abundant resources, populations rise exponentially, resulting in a J-shaped curve. As resources become scarce, population increase slows in logistic growth. When the environment’s carrying capacity is achieved, it levels off, resulting in an S-shaped curve.
When can exponential growth happen?
Exponential growth may occur for a short period if few persons and abundant resources are available. However, once the population becomes large enough, resources get depleted, reducing expansion.
When can exponential growth occur in a population?
When resources are boundless, a population might undergo exponential expansion, in which its size grows at an ever-increasing pace.
Which population is most likely to have exponential growth?
The YNP bison population peaked at 5000 animals in 2005 (Plumb et al. 2009), but if it had grown at the same rate it did between 1902 and 1915 (18 percent growth rate), there would be around 1.3 billion (1,300,000,000) bison in the YNP herd now.
What’s exponential growth?
Exponential growth is a data pattern that displays higher gains over time, resulting in an exponential function curve.
How to find the growth rate of an exponential function?
Use the formula y(t) = a__ekt to compute exponential growth, where an is the initial value, k is the rate of growth or decay, t is time, and y(t) represents the population’s value at time t.
