CalCon calculator app generated a calculator that gives you a result for a cone volume within seconds. It is easy to use, helpful, and, most importantly, free. The cone volume calculator will enable you to calculate the volume of a cone simply by entering the values of the radius and height. Whether you need the volume for a right or an oblique cone, or a truncated cone, our calculator covers it all. Steps for calculation are precise; after entering the measures, the calculator provides the result. We also have other calculators that might draw your attention, so do not hesitate to check them out.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is the volume of a cone?
A cone is a three–dimensional solid figure consisting of a flat base and a curved surface. The curved surface connects the base with the vertex. The volume of a cone expresses the amount of three–dimensional space enclosed by a flat base and the vertex, which create a closed surface. By diving into the following text, you will be able to comprehend the geometry of a cone and the mathematical equations for the volume. And, what might look like a problem to you before will now be shiny clear.
How to find the volume of a cone?
To find the volume of a cone, first, we need to have a deeper understanding of its basic components:
- The vertex is the top point of a right circular cone where the straight lines that form the lateral surface area meet, and its placed perpendicular to the center of the base,
- The vertex of an oblique cone is dragged aside from the axis that goes through the center of the base, and it is the reason for the cone’s tilted shape,
- The slant height of a circular cone (s); if we unfold a circular cone’s lateral surface area, we will get a circle sector. Therefore, the slant height is a radius of that circle sector,
- The slant height of an oblique cone is undefined. It is presumed that there are only two identical slant height lines on an oblique cone,
- The height (altitude) of a circular cone (H) is the distance between the top point and the center of the base of a cone,
- The altitude of an oblique cone (H) is the height between the top point and the plane on which the base of a cone is placed,
- The radius of a cone (r) is the radius of the base, which is, in many cases, a circle.
Values that enter the equations
We need to know the radius and height to calculate the volume. We can calculate the height of a cone (marked as H) if we know the length of a slant height of a cone, using Pythagorean theory:
s=\sqrt{r^{2}+H^{2}}Now, we do the algebraic manipulation of the previous equation to show the value of the height (H):
H=\sqrt{s^{2}-r^{2}}It is easy to calculate radius (marked with letter r) if we know the base surface area (B):
B=r^{2} * \PiAnd the value of radius (r) is:
r=\sqrt{\frac{B}{\Pi}}The volume of a cone – formula
Finally, we can proceed with the calculations as we know these basic facts about cones. Once the required measurements are obtained, we insert them into the following equation.
The equation for the volume of a cone is:
V=\frac{1}{3} * r^{2} *\Pi*HThe SI unit of volume is a cubic meter (m^{3}) . The Metric system also includes the liter (l), which is a special name for the cubic decimeter (dm^{3}) . But, do not get confused about units if you encounter others not mentioned here. It is possible that they just used prefixes to manipulate the result, or it is another area’s system of measurements. Also, some of the units for the volume have been improved or neglected through the years. However, if you want to know more about volume units, you can check it out on our Volume Calculator.
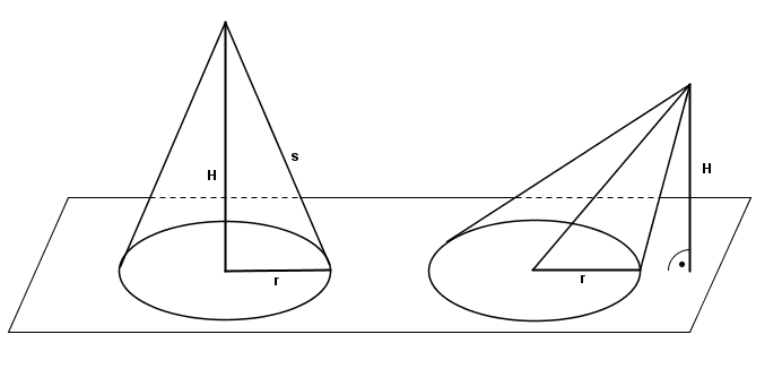
In the picture above, the right circular cone is displayed on the left side and an oblique cone on the right side.
Oblique cone volume
We can acknowledge the main difference between the right circular and an oblique cone based on the previous facts, and it is in their geometry. The rotation of a right triangle makes a right circular cone. With this in mind, we should picture the moving of a right triangle so that a hypotenuse creates a lateral area surface, and one of its other sides the radius of the base while the other serves as height. So, the straight line that goes through the vertex and the center of the base is the axis of a cone. In sum, this is why the vertex of a circular cone is perpendicular to the center of the base, which is not the case with an oblique cone.
In plain words, an oblique cones vertex is not congruent with the axis of a base. To calculate the volume of an oblique cone, we use the formula given above in the section The volume of a cone, formula.
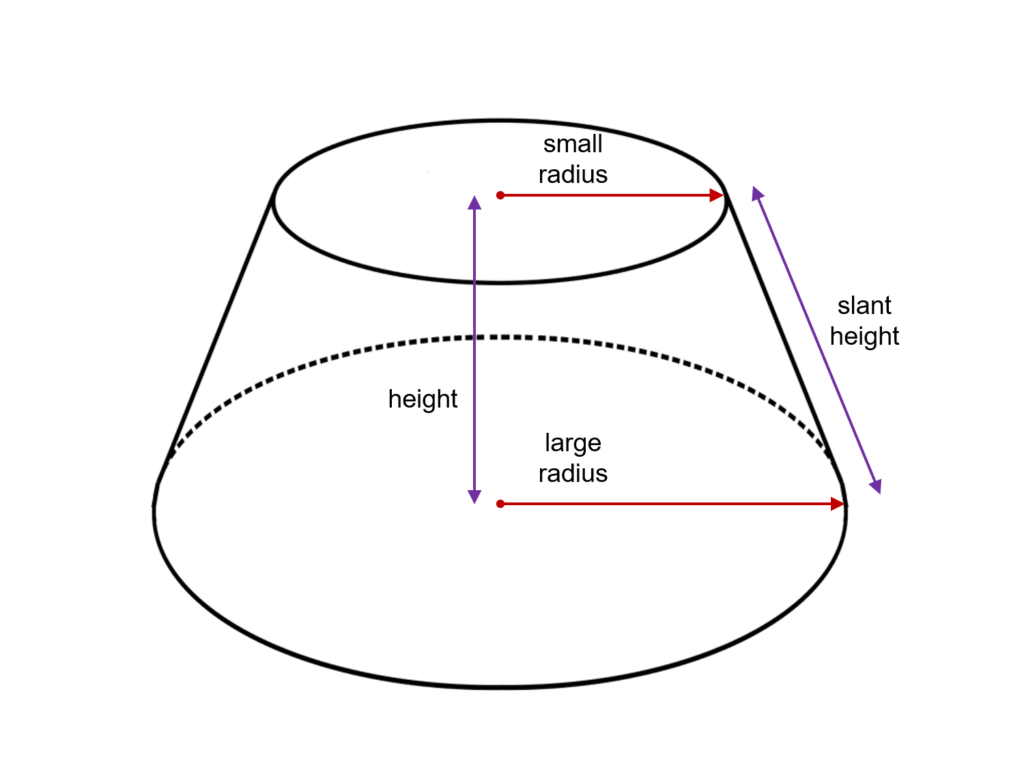
The volume of a truncated cone
How to make a truncated cone?
To truncate applies to shortening. We do this by eliminating the upper part of a cone (which contains the vertex). To explain this process, we need to visualize a plane parallel to a base, which cuts off the upper part. Even though the upper part remains cone-shaped, it becomes smaller. So, the other part, called a frustum, is limited with the base and the circle that appeared due to a parallel plane cutting off a piece of a cone. In consequence, the lateral surface area of the frustum is the area without the circles. The origin of the word frustum is borrowed from Latin, and it stands for a piece cut off. The plural of that word would be frusta.
Truncated cone volume (volume of frustum-formula)
There are two ways to do the math when calculating frustum volume. The first is to calculate the volume of the piece taken away and subtract it from the volume of the whole cone (measured before cutting). The result is the volume of the frustum. It is possible to use this if you do not know the formula, but we are here to help and provide you with a detailed calculation. The formula for the volume of the frustum is:
V=\frac{H*\Pi}{3}*(R^{2}+R*r+r^{2})R-radius of the base of the bigger circle
r-radius of a smaller circle
H-height of the frustum
FAQ
How do I calculate a cone volume by hand?
You can calculate a cone volume in three steps:
1. Find the radius (r). If you know the measure of the diameter, divide it by two to get the value of the radius or approach to measuring by a ruler.
2. In this step, determine the value of height (H). If the slant height is known, you can use Pythagorean theory or take a ruler to measure it and write it down.
3. Use these values in the formula for volume V=\frac{1}{3} * r^{2} *\Pi*H
How to find the volume of a right circular cone?
The right circular cone is a three-dimensional solid figure whose volume is quantified numerically as one-third of the product of the base area and its height.
What is the relationship between the volume of a cone and a cylinder?
We need to have a cone and a cylinder with matching heights and radiuses to make the proper comparison. After calculating their volumes, we will encounter that the volume of a cone can fit three times into the volume of a cylinder.
Interesting facts: The pyramid and the prism have the same relationship with their volumes. As the number of the sides of the pyramid starts to grow, the pyramid looks more like a cone. Also, a prism looks more like a cylinder as the number of its sides increases, so we can say that the cylinder is a “circular prism.” The volume relationship of a cone, sphere, and cylinder: If a cylinder has the same dimensions for the height as the diameter of its base, then we can fit both the cone and the sphere inside the cylinder.
What is the volume of a cone with radius one and height three?
The volume equals the \Pi . By definition, \Pi is the ratio of the circumference of a circle to its diameter ( \Pi=3.14159265 ).
How to find a volume of a cone in cubic inches?
For example: If your measures are given in meters, convert them into inches. The length of 1 meter equals the length of 39.3700787 inches. While using the formula for the volume of a cone, as multiplying the numbers, their units will also multiply, and you will get cubic inches.
How do I calculate volume?
You can calculate the volume by multiplying the dimensions of a three-dimensional figure’s length, height, and width.
