Tangent of a Circle Calculator with steps

Using our Tangent of a Circle Calculator, get the tangent length segment when a secant and tangent intersect from a location outside the circle. A tangent to a circle crosses at a certain point, i.e., the radius at that angle. The product of the lengths of the secant and its external segment is equal to the square of the tangent segment length if a secant and a tangent of a circle connect outside the circle from a point.

While you are here, you should see our other categories like statistics, where you can calculate Average Rating or maybe you are interested in the Exponential Distribution Calculator.

Take a look other related calculators, such as:

What is a Tangent?

The tangent line to a curve at a point is the straight line that most closely approximates (or “clings to”) the curve near that point in geometry. As the second point approaches the first, it can be regarded the limiting position of straight lines going between the supplied point and a neighboring point of the curve. If two curves have the same tangent line at a point, they are tangent. The tangent plane to a point on a surface and two tangent surfaces at a point are both defined in the same way.

The tangent of an angle is the ratio of the side opposite the angle to the side adjacent in right triangle trigonometry. Also, the tangent (ratio) value is determined only by the magnitude of the angle, not by the right triangle utilized to compute it.

Tangent of a Circle – Definition

A tangent to a circle is a straight line that passes through the circle’s center at one point, known as the point of tangency. The tangent of the circle is perpendicular to the radius at the point of tangency. Tangents are linked to three theorems (unfortunately, do not explain crop circles). But, like so many crop circle makers skulking down a tangent route (a tangent is tangential to a radius), we’ve already sneaked one past you.

The Two Tangent Theorem is the name of the second theorem. It says that two tangents of the same circle drawn from the same point outside the circle are congruent. Finally, the Tangent Secant Theorem illustrates the link between a circle’s tangent and secant.

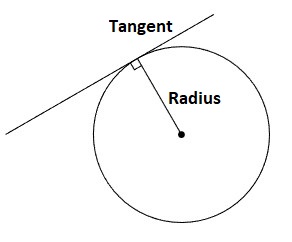
Equation of Tangent to a Circle

A circle had a radius of r unit and a center C(a,b). D(x,y) is a point on the circle’s circumference, and the equation of a tangent to a circle equation is:

(x-a)^2+(y-b)^2=r^2

A tangent is a straight line that only touches the circle’s circumference once. At D, the tangent line AB intersects the circle. At the point of contact D, the radius of the circle CD is perpendicular to the tangent AB.

It depends on the sort of circle you have (is the center at the origin?) and the type of tangent you want. There are three tangent equations for a circle: point form, slope form, and parametric form. Let’s look at a typical scenario: A circle with a radius of r and its center at the origin. Such a circle’s equation would be:

x^2 + y^2 = r^2

Tangent of a Circle Formula

Let’s have a look at the tangent equation now. A tangent is a line, and we need two things to form a line’s equation:

The incline (m),
A point on the line.

The tangent to a circle has the following general equation:

The first equation for the tangent to a circle:

x^2 + y^2 = a^2

The second equation for the tangent to a circle:

xa_1+yb_1=a^2

The length of a tangent is given by the following formula:

l = \sqrt {d^2-r^2}

Tangent of a Circle Calculator – How to Use?

To get the tangent of a circle at a given point, do the following:

Input the circle’s radius r.
Next, calculate the distance d between the center and a tangent point.
The length of the tangent l will now be calculated for you by the tangent of a circle calculator. Also we have several other calculators from math.

Tangent of a Circle Calculator – Example

Let’s try to tackle a genuine tangent of a circle problem now that you know what a tangent of a circle is. First, calculate the length of the tangent of a circle with a radius of 10 meters and a point on the tangent that is 15 meters from the center. To get the length of a tangent, use the following formula:

Insert the circle’s radius, r = 10 m.
Then, enter 15 meters as the distance between the center and the tangent point, d.
Using the formula for the tangent of a circle:

$l = \sqrt {d^2 - r^2} = \sqrt {225-100} = 11.18$ m.

Tangent of a Circle – Real-world Applications

Many real-world applications and disciplines of study, including building, gardening, and engineering, can benefit from circles and tangent lines. Lines that touch or cross circles come in various shapes and sizes. Each of these lines has its own set of features and connections to a circle.

By creating a right triangle with the radius and confirming that it is a right triangle with the Pythagorean Theorem, you demonstrate that a line is a tangent to a circle. To be tangent, the slopes of a line and the radius drawn to the possible point of tangency must be negative reciprocals. The segments are congruent if tangent to the same circle and begin from the same exterior point.

FAQ

What is a tangent of a circle?

A tangent to a circle or curve is a line or line segment that only touches the circle at one point. The tangent of a circle is perpendicular to the radius drawn to the tangent point.

How do you find the tangent of a circle?

The tangent runs perpendicular to the radius that connects the circle’s center to point P. The tangent’s equation will be of the form $y = m x + c$ because it is a straight line.

What is the relation between the secant and tangent of a circle?

When a tangent and secant segment are drawn to a circle from an exterior point, the square of the tangent segment’s measure equals the product of the secant segment’s and its external secant segment’s measurements.

How many tangents are in a circle?

A tangent is a line that touches a circle at just one point. A circle can have an unlimited number of tangents.

Tangent of a Circle Calculator