Arccos Calculator (Inverse Cosine)

Inverse cosine(arccos) calculator enables you to calculate arccosine of any value you wish. One of the most important subjects of algebra is trigonometry. Trigonometry, a branch of mathematics, studies angles, relationships between angles and sides, and sides of the triangles. For instance, inverse cosine changes values of the x-axis and y-axis. It does this by swapping x and y. In the case of inverse sine, we trade the y-axis and y-axis. If you have ever wondered how to calculate the arccosine, you can use this calculator and follow the process step-by-step.

What is the inverse of cosine?

The inverse of cosine is arccosine or cosine^-1. To get inverse of cosine we invert, swap, x and y axises. The arccosine is an inverse function. In most cases, most operations have an inverse function. To understand inverse functions better, we can take addition as an example. The inverse process of addition is subtraction. By the same rules, the inverse function of cosine is arccosine(inverse cosine). We use inverse cosine to solve complicated problems.

In retrospect, in right-angle triangles, cosine is the ratio of the side adjacent to the angle divided by the hypotenuse. For example, the figure below is a right triangle. On it, we can see what exactly is cosine:

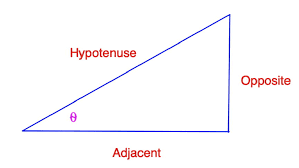
The cosine angle we are looking for is” Theta.” We first get “cosine” when we divide the adjacent side of the triangle with hypotenuse. Because cosine’s codomain is [1,-1], arccosine can only calculate in that domain.

Inverse cosine graph

The cosine graph is one of the most critical graphs in mathematics and science. The cosine graph is a simple-periodic function. To find cosine, we use the formula:

\cos(\theta)=\frac{Adjacent}{Hypotenuse}

The cosine graph is in the figure below. In specific points cosine of the angle is equal to zero. For example, if x = 90 degrees (or pi/3 radians) then cosine is zero. The same can be said for x = 270 degrees(or 3pi/3 radians).

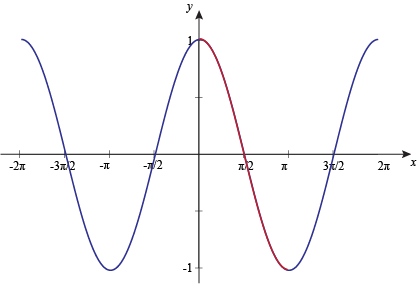
We get an inverse cosine graph by switching two axes. To sum up, when we invert function cosine, we reverse the x-axis and y-axis.

Unlikecosine’ss graph where cosine’s at if x = 90 or 270, cosine is zero, in the case of inverse cosine, if x = 180 degrees or 360 degrees, arccos is zero.

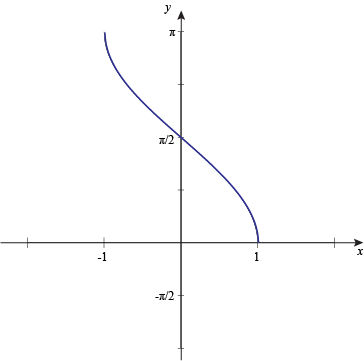
Inverse cosine – Examples

For our first example, we are calculating the arc cosine of one-half. We are most likely to solve angles in the unit circle in most situations. The unit circle is a circle with the essential tips. We can read all the arccosine, cosines, and cosine’s trigonometric functions with it.

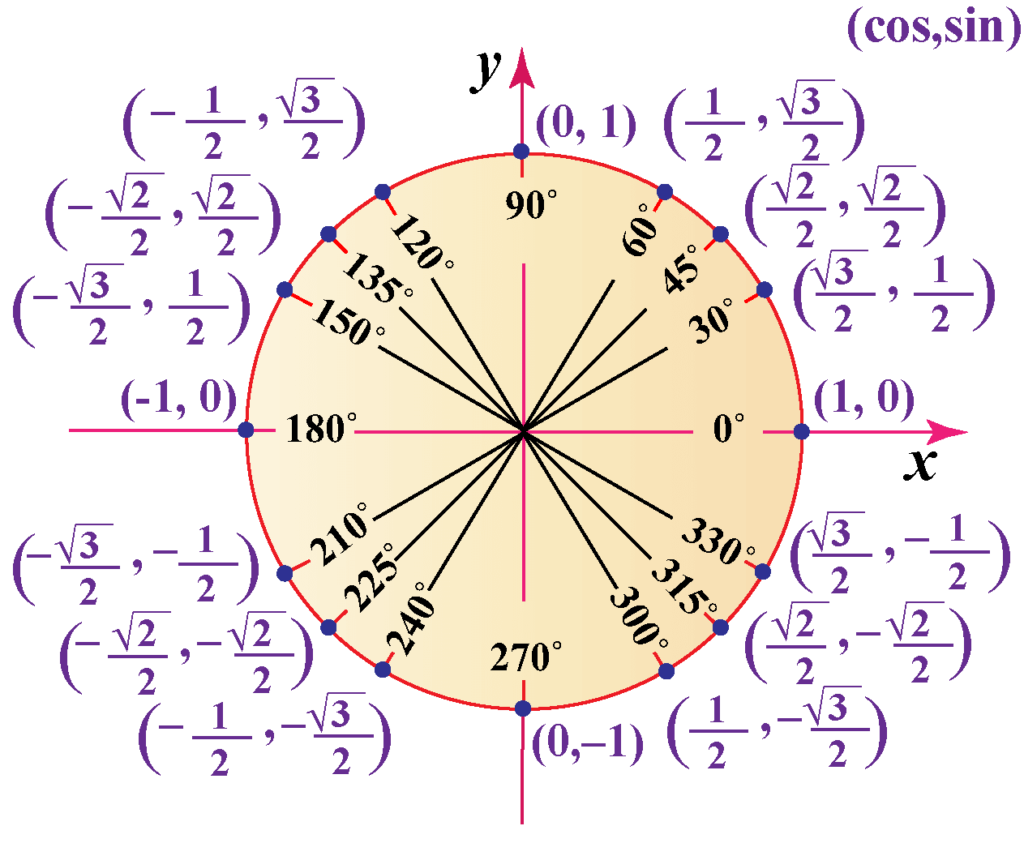
From the figure, we can see that the arc cosine of one half is 60 degrees. In some tasks, you might have to figure out the answer in radians. So how do we get to radians from degrees? To do that, we use the formula.

x \times 360 \degree = 60 \degree \times 2 \pi

X is unknown radians, and pi is a constant (pi = 3.14).

In our next example, we will calculate arc cosine without the help of the unit circle. Let’s say that we haveLet’soblem to solve. Problem: Calculate the arc cosine of 2/3 (two-thirds). First of all, we are going to divide two-thirds. We get x = arccos(0.667). To figure out this problem, we can draw a triangle. This triangle will have a hypotenuse equal to

\cos(x) = \frac{b}{c}

\frac{2}{3} = \frac{b}{c} => 2c = 3b => c = \frac{3b}{2}

Where c is hypotenuse and b is the adjacent side. Now we can use the formula for cosine. Our adjacent side is b = b, and our hypotenuse is c = 3b\2. We should now calculate the cosine of Theta. Then we can estimate that the arc cosine of a given task is around 48 degrees.

\cos^{-1} [\cos(x)]= x = \cos^{-1}\left ( \frac {b}{c} \right )

In addition, we have some special cases of cosine and inverse trigonometric functions. For example, if we have cosine of x is equal to -1. In this case, we can use the unit circle to determine the arc cosine of (-1). arccos(-1) = x = pi. As previously mentioned pi is a constant. Pi is equal to 3.1415… Cosine has a value of zero for two angles, pi/2 + k*pi. When cosine is zero inverse cosine is equal to pi/2 + k*pi. Where k = (1,2,3…). We often use this way of writing functions. The reason is quite simple. Cosine is equal to zero for pi/2. However, it is also equal to zero for 3pi/2, and for 7pi/2… The constant k makes sure that we take all the possible outcomes for cosine of x.

Derivative of inverse cosine

The derivative (or extract) of a function f(x) near the region of dot x is called a limit value.

f'(x) =  \lim_{h\to\infty}\frac{f(x+h)-f(x)}{h}

Suppose it exists final or infinite. Usually, we use ” (x) to mark a derivation near the x region. A tabular derivation of inverse functions is the most common derivation for all trigonometric functions. For example, derivation of arc cosine would be

(\arccos(x))'=\frac{-1}{\sqrt{1 - x^2}}

The difference between the derivation of inverse cosine and sine is in minus. So we can write.

-(\arccos(x))' = (\arcsin(x))'

FAQ