A Cylindrical Coordinates Calculator is a converter that converts Cartesian coordinates to a unit of its equivalent value in cylindrical coordinates and vice versa. This tool is very useful in geometry because it is easy to use while extremely helpful to its users. A result will be displayed in a few steps, and you will save yourself a lot of time and trouble. You should also see our related Spherical Coordinates Calculator, for the conversion between spherical and rectangular systems.
In the following text, you will learn how to draw and determine the location of a point in a three-dimensional space. Also, we will provide mathematical formulas and examples of calculations that are necessary to gain basic knowledge in this field. Now, let’s approach our topic.
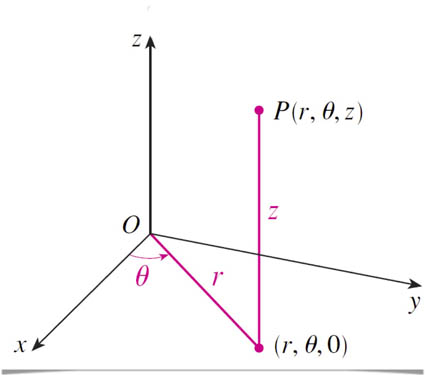
What is a Cylindrical Coordinates System?
A cylindrical coordinate system is nothing else but an extended polar system. That means that we create a three-dimensional system by adding the third axis to the polar system. Unlike the Cartesian coordinate systems, which is a system that provides a pair of numbers for each point that represents the distance from axes depicted by (x, y, z), cylindrical coordinates are depicted by (r, \theta – theta, z). These three values represent:
- The radial distance r or ρ is the distance from the z-axis to the point.
- The \theta – theta is the angle between the reference direction on the chosen plane and the line from the origin to the projection of the point on the plane.
- The height z is the distance from the chosen plane to the point.
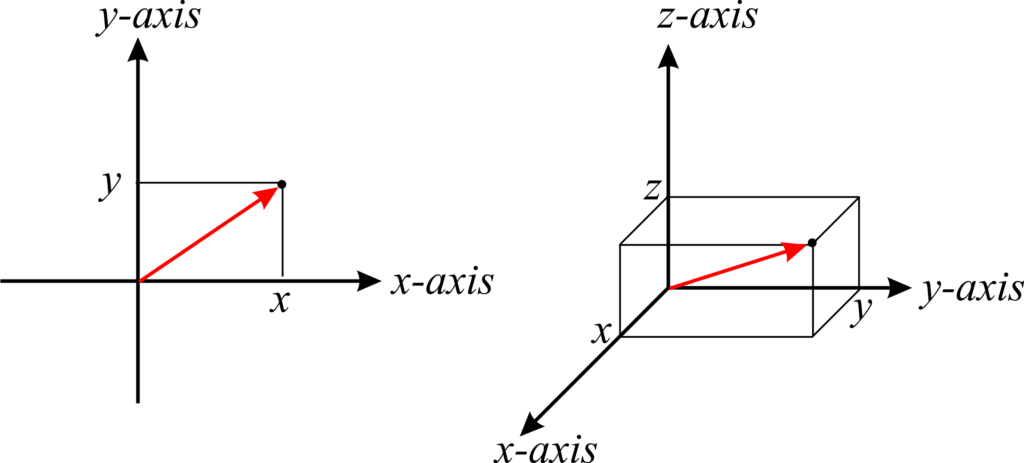
What is a Rectangular Coordinates System?
A rectangular coordinate system is two-dimensional, and it is made of two number lines that intersect under the right angle. Each point in this system is determined by a pair of numbers (x, y), where x is the distance from the origin (0, 0) and is measured on the x-axis, and y is the position on the y-axis.
Also, on the right side of the x-axis are positive numbers, while on the left side are negative numbers. In contrast, positive numbers are on the upper side of the y-axis, while negative on the other side.
Conversion formulas
Our calculator enables you to convert cylindrical coordinates into Cartesian and vice versa. Now, we will demonstrate the process that occurs when you choose what type of conversion you need and enter the position of the given point. The best way to show how much our calculator saves you from math is to show the formulas on which the calculator operates.
Rectangular to cylindrical coordinates
If we want to convert rectangular (x, y, z) to cylindrical coordinates (r,\theta, we need to use the following equations:
- r=\sqrt {x^{2}+y^{2}}
- \tan\theta=\frac{y}{x}
- z=z
Cylindrical to Cartesian – rectangular coordinates
If we want to convert cylindrical (r, \theta, z) to Cartesian coordinates, we need the following equations to do the conversion:
- x=r \cdot \cos \theta
- y=r \cdot \sin \theta
- z=z
Since the trigonometric functions are in the formulas, if you have any difficulties regarding that, see this Trigonometric Functions Calculator, which will help you for sure. In addition, there is an Angle Conversion tool to help you convert between different units.
How to use the Cylindrical Coordinates Calculator?
This calculator is created to guarantee its simple utilization. However, if you find some difficulties managing our application, follow the steps listed below:
- Determine what sort of conversion you need and click on it.
- After that, input the data (values of the coordinates) of the point that you have.
- The rest of the calculation does our calculator, and you have the result within seconds.
Practical Example
Convert the rectangular coordinates (7, 2, 4) into their equivalent cylindrical coordinates.
r=\sqrt{x^{2}+y^{2}}=\sqrt{7^{2}+2^{2}}=7.28 \theta=\arctan\frac{y}{x}=\arctan\frac{2}{7}=15.94 \degree z=z = 4The new coordinates are (r, \theta, z)=(7.28, 15.94°, 4). In order to do some control, you can change the input values to be cylindrical coordinates and do the calculation of Cartesian.
Geometry is a very wide area. It has a vast range of mathematical problems, and the CalCon team endeavors to cover them via our articles. A cylindrical coordinates calculator is one of them, and it allows you to save time while calculating the position of a point.
FAQ
What are cylindrical coordinates?
To create cylindrical coordinates, we need to add a third axis to make the system three-dimensional. In other words, it is an extension of two-dimensional polar system to three-dimensional.
How to convert cylindrical coordinates to rectangular coordinates?
It is possible to convert cylindrical (r, \theta – theta, z) to rectangular (x, y, z) coordinates by using the formulas given below:
x=r \cdot \cos \theta
y=r \cdot \sin \theta
z=z
What is the radial distance?
It is the Euclidean distance from the origin O (0, 0) to the point in three-dimensional space.
How to graph xyz coordinates?
To find a point (x, y, z) in three dimensions, we use the following steps:
Find the value of x on the x-axis, and from that point, moving parallel to the y-axis, move for the value of y. Now, from that point, moving parallel to the z-axis, move for the value of z, and that is your point.
Curl in cylindrical coordinates?
The infinitesimal rotation of the vector is represented as the curl of a vector.
How to convert spherical coordinates to cylindrical?
The difference between spherical (p, \theta, \phi) and cylindrical coordinates is in the third one \phi which is the angle of elevation to the point, and p is the distance between the origin and the point being described.
