Mathematics is a complex science but applicable in almost all segments of everyday life.
If you are a fan of math and want to learn more about the ellipsoid and how to determine the volume, you are at the right place. On the other hand, if you are not a fan of math and need help with determining the volume of an ellipsoid, you can use our calculator.
Take a look other related calculators, such as:
- Phase shift calculator
- 30 60 90 triangle calculator
- 45 45 90 triangle calculator
- Power reducing formula calculator
- Probability calculator 3 events
- Cofunction calculator
- Sum and difference identities calculator
- Trigonometry calculator
- Segment addition postulate calculator
- Fundamental counting principle calculator
- Condensing logarithms calculator
- Population density calculator
What is ellipsoid
For an ellipsoid, we can say that it is a body whose all plane sections through one of the axes are ellipses, and all other sections are ellipses or circles. The best example is the example of planet Earth.
The Earth has the shape of a geoid, a body similar to a rotating ellipsoid.
Imagine a sea surface that passes beneath all land, and you will get a geoid. As the Earth’s surface is shown on maps, the geoid needs to be approximated by an ellipsoid. An ellipsoid is formed by rotating an ellipse about a shorter (polar) axis.
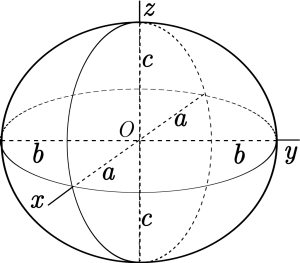
Another key point is that an ellipsoid is a second-order surface or a centrally symmetric surface. In the center of the ellipsoid, three mutually perpendicular axes (main axes) of symmetry intersect. Two of these axes define three mutually vertical planes of symmetry. If the significant axes are taken as coordinate axes, the ellipsoid equation reads:
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1where a, b and c are the semi-axes of the ellipsoid.
How to calculate the volume of an ellipsoid?
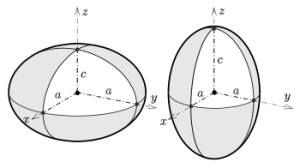
Notably, all are plane cross-sections of an ellipsoid. Two strands of parallel planes have circular cross-sections with the ellipsoid. A rotating ellipsoid is created by rotating an ellipse about one of its axes, with two equal semiaxes (for example, c = b). The volume of the ellipsoid is:
V = \frac{4}{3}\cdot \pi \cdot a\cdot b\cdot cHow to use the ellipsoid calculator?
All you need to determine the volume of the ellipsoid are semi-axises.
To point out, here is an example of calculating the volume with the help of our calculator.
We have an ellipsoid whose semi-axis A is 5cm, semi-axis B is 8cm and semi-axis C is 6cm.
We want to calculate its volume expressly.
The calculation formula is:
V = \frac{4}{3}\cdot \pi \cdot a\cdot b\cdot cIt follows from this formula that the volume of this ellipsoid is equal to:
V = \frac{4}{3}\cdot 3.14 \cdot 5\cdot 8\cdot 6 = \frac{3014.4}{3} = 1004.8 cm^{3}As a result, you have that a volume of the ellipsoid is equal to 1004.8 cm3.
Real-life applications
In the first place, a reference ellipsoid is a surface that approximates a geoid in geodesy. Moreover, in the context of standardization and geographical applications, the geodetic reference ellipsoid is a math model that you can use as the basis of spatial reference systems or definitions of geodetic data.
In 1687, Isaac Newton published Principio. He included evidence that a rotating self-gravitational fluid body in equilibrium has the shape of a flattened ellipsoid generated by an ellipse rotated around its small diameter. That shape he called a flattened spheroid.
Generally speaking, it is important to realize that many ellipsoids have been used to model the Earth in the past. In the first place, planet Earth was showing with different assumed values of a and b and different assumed center positions and different axis orientations relative to solid Earth. To demonstrate, the primary use of reference ellipsoids is the basis for the latitude (north/south), longitude (east/west), and ellipsoidal height coordinate systems.
