If you need to find the area of a sector, you’ve come to the right place. Here we will learn what a sector is and how to use the sector area calculator.
Take a look other related calculators, such as:
What is a sector of a circle? Sector definition
A sector is a geometric figure surrounded by two radii and bounded by the arc of a circle.
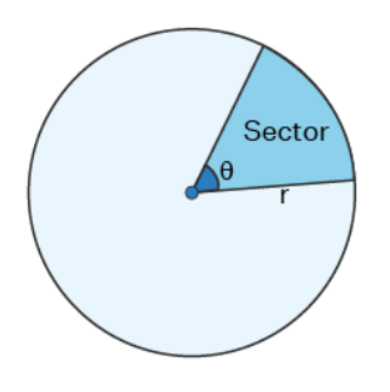
The previous image shows an example of a sector.
In the previous image:
- 𝛳 is a central angle
- Two straight lines connected at the center are called radii (they represent a radius). It is a line connecting a circle’s midpoint and its exterior. It is equal to one-half of the diameter.
- A curved line is an arc of the sector.
An arc is a part of the circle’s circumference.
Area of sector formula: How to find the area of a sector
The area of a sector is the region enclosed by the two radii of a circle and the arc. For easy computing, the area of the sector, radius, and central angle is used. Angles can be denoted in degrees or radians. Radians are often used in mathematics. Depending on the unit of the angle, there are two formulas for calculating the area of the sector.
If you use radians as the unit, the formula is:
A = \frac{\theta \cdot r^{2}}{2}If you use degrees as the unit, the formula is:
A = \frac{\theta}{360}\cdot \pi \cdot r^{2}In previous formulas:
- A is an area of the sector
- 𝛳 is a central angle
- r is a radius
- 𝜋 is a mathematical constant and is equal to 3.14159265359
Unit for the area in meters squared or m^{2}.
Previous formulas are derived from a simple connection between radians and degrees:
\pi_{ } radians= 180^{\circ }It follows that:
1 radian= \frac{180^{\circ }}{\pi}For example, let’s calculate the area of a sector with a radius of 2 cm length and a central angle of 40°. So, we have:
r = 2\:cmSince the unit of the angle are degrees, we will use the following formula for calculation:
A = \frac{\theta}{360}\cdot \pi \cdot r^{2} = \frac{40}{360}\cdot \pi \cdot 2^{2} = \frac{40}{360}\cdot 3.14159 \cdot 4 = 1.396\:cm^{2}
The area in our example is equal to 1,396 centimeters square.
Special cases: area of semicircle, area of quadrant
The amount of space restricted within the boundary of a semicircle is called the area of a semicircle.
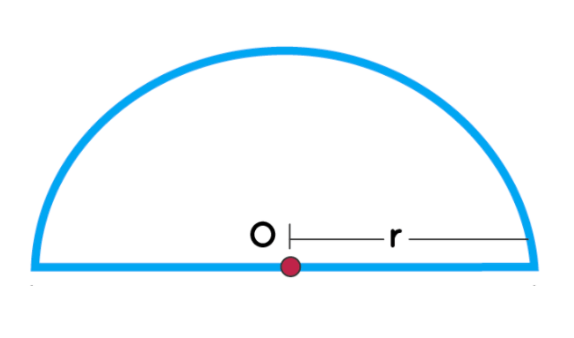
A semicircle is half of a circle. Thus, the area of a semicircle is half the area of a circle. Since the area of a circle is equal to r^{2}\cdot \pi, it follows that the area of the semicircle is:
A = \frac{ r^{2}\cdot \pi}{2}The Area of a Circle Calculator contains more information about computing this value for a circle.
A quadrant is a one-fourth part of the circle. Two quadrants are equal to semicircles. Similar to a semicircle, the area of a quadrant is equal to one-fourth of the area of a circle. Therefore, the area of all the four quadrants is equal, and the sum of areas of the four quadrants is equal to the area of the circle. The image below shows the quadrant.
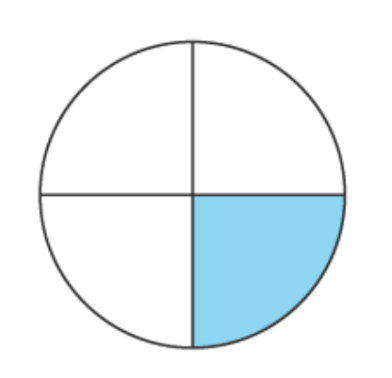
You can calculate the area of the quadrant using this formula:
A = \frac{ r^{2}\cdot \pi}{4}We can also derive this formula from the segment area formula since the quadrant is basically a sector with a central angle of 90°. According to that, it follows:
A = \frac{\theta}{360}\cdot \pi \cdot r^{2}=\frac{90}{360}\cdot \pi \cdot r^{2}=\frac{1}{4}\cdot \pi \cdot r^{2}Sector area calculator – when it may be useful?
This calculator can be useful when calculating the area of a segment. A segment is a figure in geometry formed when a triangle enclosed by two radii and a chord (or secant) is subtracted from the sector of a circle. A line segment connecting any two points on the circle’s circumference is called a chord. The longest chord is the diameter, and it passes through the center of the circle.
A segment is an area enclosed by a chord and an arc in math. The largest segment in any circle is a semicircle formed by the diameter and the corresponding arc. Segments are often used in geometry. There are two theorems based on the segments:
- Angles in the same segment theorem
- Alternate segment theorem
FAQ
How do you calculate the area of a sector?
The radius and central angle of a circle are used for calculating the area of a sector. You can easily input these values using the calculator, and it will calculate the result. If these parameters are known, calculate the area by using the following formula if the unit for the angle are radians:
A = \frac{\theta \cdot r^{2}}{2}If the unit for the central angle is degrees, use this formula for calculation:
A = \frac{\theta}{360}\cdot \pi \cdot r^{2}What is the area of the sector of the circle?
The area of a sector is the region enclosed by the two radii of a circle and the arc. You can compute it easily using radius and central angle. Since a sector is a portion of a circle, the area of a sector is a fraction of the area of the circle.
