What is a central angle? It sounds like something you’d learn in a high school geometry class, and chances are, you did, but you forgot about it, just like most other math lessons from high school. However, it’s useful to know that this concept of math has real-world applications, too! While the formula for finding the measure of a central angle might seem intimidating at first, we’ll break down each part step-by-step so you can learn what it’s all about. Before we get into the nitty-gritty details, though, let’s start with a definition.
Take a look other related calculators, such as:
What is a central angle?
A central angle is an angle formed by two radii of a circle. It can be any size you want, so long as the radius stays constant.
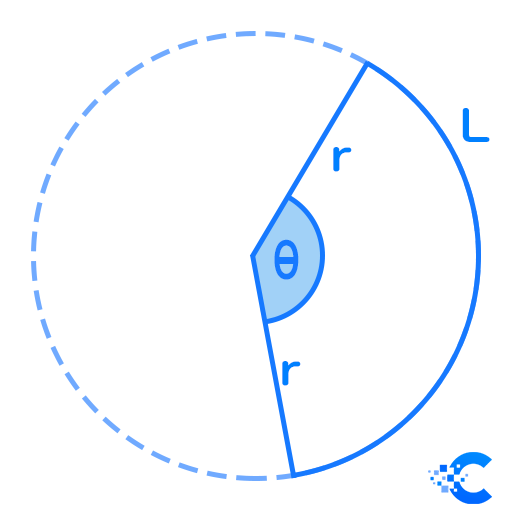
To find the central circle, draw two lines that are equal to the radius, that go from the center of the circle to the outer layer. This will give you two points on the circle, A and B. Draw an arc that connects those two points, and you have your central angle, AOB.
Where does the central angle formula come from?
Why is it called the central angle formula? Well, it comes from a trigonometric identity called “the law of cosines,” which means that if you have two sides of a triangle and the angle between them, you can use this identity to figure out what the third side would be.
The law of cosines is derived from the Pythagorean Theorem, from which we know that:
a^2 + b^2 = c^2 \text { (for right triangles)}Central angle formula
The central angle formula is very simple:
\theta = \frac {l}{r}L is the length of the arc, and r is the radius. Keep in mind, that the result you get from this is in radians, so you might need to convert it to degrees if that is what you need.
How to find the central angle of a circle?
In order to find the central angle of a circle, you have to follow a few simple steps:
- Find the radius of the circle. The radius is a line segment that extends from any point on a circle to its center.
- Calculate the distance between the two radii within a circle, called an arc.
- Take this number, divide it by the radius, and you will get your central angle in radians.
Central angle formula explanation
The central angle formula is pretty simple:
CA = \frac {l}{r}L is the length of the arc, and r is the radius of the circle.
The central angle of a circle is equal to the quotient of the length of the arc and the radius.
How to use the central angle calculator
Our central angle calculator uses the formula that we mentioned above. So, in order to calculate the central angle using this calculator, all you need to do is enter the arc length and the radius of the circle (in any measurements you want), and you will get the central angle.
The central angle can be calculated in any measurements you want, from standard degrees or radians to gradians, turns, minutes of arc, and more.
Central angle example
The central angle in a circle is the angle at the center of the circle, formed by two radii. The central angle in a square, equilateral triangle, or rectangle is a right angle. A right angle has an inscribed arc that forms 1/4th of its circumference.
FAQ
What is the central angle?
A central angle is an angle formed by two radii of a circle.
How to find a central angle with arc length?
You can calculate it using the formula we mentioned above: CA = l/r, where l is the arc length and r is the radius of the circle.
What is an arc length?
The arc length is the distance between the two points on the outer layer of the circle that form the central angle.
