The Average Rate of Change is a statistical measure of the rate of change of a variable, with the average change over a period of time. This statistic is used to measure variable volatility and is commonly used in finance and economics.

This article will help you navigate the world of average rates of change. You will learn about the different types of average rates of change and how to calculate them. If you are interested in how to calculate the arithmetic mean or average, you can do it with an Average Calculator.

Take a look other related calculators, such as:

Average Rate of Change – What is?

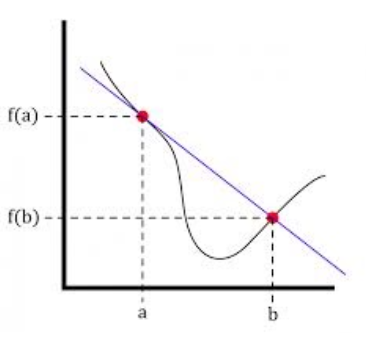
The easiest way to determine the average rate of change is to display the value within one function, relative to another. You can use the average rate of change to determine the slope of the graphical function. The slope is a straight line, and it connects the endpoints of the interval shown in the graph. The average rate of change is a function that you can apply to calculate the rate of change in a given time frame.

Average Rate of Change Formula

The following chart will better show you the positions of the points to understand how to find the average rate of change.

Graph of the average rate of change
Graph of the average rate of change

This formula will help you calculate the average rate of change:

\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}

The coordinates of the first point are (x1, f(x1)), while the coordinates of the second point are (x2, f(x2)).

With the help of the formula, you can calculate the slope of the line. You can do it by taking the difference in the value of this side of the line and dividing the difference into two time periods. As steep as the line is, it represents a slope measure.

For instance, if there is a line with a slope of 2, it means that for every 1 unit of distance, the line will move 2 units in the same direction. The slope will be a positive number if the line goes up and a negative number if it goes down.

Instantaneous Rate of Change and Average Rate of Change: Difference?

These are two different measurements of how a function changes over time. They both use the same data but give a different function view.

The instantaneous rate of change is the slope of a curve at a specific point. In the simplest terms, the instantaneous rate of change is when a quantity changes at a particular instant in time. The most common way to measure this values is by using the slope of a line on a graph. You can use a line with a slope to find the instantaneous rate of change. The slope of a line is the vertical change divided by the horizontal change.

For example, if the value of a variable is 11 at the beginning of an interval and 12 at the end, the slope would be 11/12 = 0.9167. If you know the slope and the two points on the line, you can calculate the instantaneous rate of change.

The average rate of change is the slope of a curve over a specific interval. You can calculate the line slope that connects the two dots on the curve representing the interval’s start and end. You can calculate it by dividing the total difference by the total time.

Average Rate of Change – How to Calculate?

We have developed many free calculators that make your life easier every day, and one of them is the Average Rate of Change Calculator. For calculation, you need to divide the current and previous values by the number of periods.

The rate of change is the measure of how fast something changes. If you consider investing in a company, the rate of change is the number that tells you how much the company’s worth has changed over a certain period. To calculate the rate of change, you need to know two things: the starting value and the ending value.

To calculate the rate of change, divide the difference between the starting and ending values by the starting value. If your starting value is $1,000 and your ending value is $1,500, your rate of change is 50%.

Our average rate of change calculator is very easy for user. You need to know the first coordinate point and the second coordinate point for the calculation. You need to enter the values, and our calculator will calculate them, and your results are there.

Average Rate of Change Calculator – Example

Let’s say the user is looking for a definition of “average rate of change over an interval.” The user should know that the average rate of change over an interval is the average of the slopes of the curve over the interval. For instance, you can calculate the average rate of change over an interval for a function of y = 2x+3  by dividing the change in y by the change in x, which equals 3.

First example

You have the following feature set:

f(x) = x^{2} + 6x - 8

Find the average rate of change in a given interval [-5, 7]?

You need to find the values of the given function for both points, as follows:

f(-5) = (-5)^{2} + 6\cdot (-5) - 8 = -13

f(7) = (7)^{2} + 6\cdot (7) - 8 = 83

Third, enter the values in the equation.

A = \frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} = \frac{83-(-13)}{7-(-5)} = \frac{96}{12} = 8

With the help of our new calculator, you can enter these values to check the result.

Second example

To calculate the average rate of distance change, we need to understand what a distance is. A distance is a measurement equal to the shortest distance between two points. A step is a unit of measure equal to the length of one foot.

We must also understand what a step is. A step is a unit of measurement equal to the length of one foot. So, to calculate the average rate of change of distance, we must first calculate the sum of the distances and divide it by the number of steps.

When calculating the average distance speed over time, the essential variables are the distance and time changes. Suppose you are given the coordinates for the first point (0, 0) and the coordinates of the second point, the distance between the two cities, and the time of that trip (1320.5, 13.5). You can calculate this as follows:

A = \frac{1320.5-0}{13.5-0} = \frac{1320.5}{13.5} = 87.81

FAQ

How to find the average rate of change?

The average rate of change is a mathematical formula that calculates the average of the change in the data. You can calculate by dividing the total change by the total number of data points.

Find the average rate of change over a particular interval?

The best way to find this values is by using the slope of the tangent line. The slope of the tangent line equals to the change in y over the change in x. 

What is the average rate of change formula?

You can use this formula: A = [f(x_2) - f(x_1)] \div (x_2 - x_1) . 

How do you find the average rate of change between two points?

You find the average rate of change between two points by taking the slope of the line. The best way to calculate the slope of a line is by taking the vertical change and dividing it by the horizontal change.