Volume Conversion Calculator allows you to convert one volume unit to another. Based on your input value, this calculator will use the values from the volume conversion graph and convert the volume unit you selected to 8 other volume units that you specify. In addition, you can choose from the huge list of available units such as cubic meters, litres, cubic inches, gallons, cups, tablespoons, quarts, pints and more. Our calculator is also available as an app for smartphones, thus have it on the list of the best free apps you use daily.

Check out math category if you need more math-related measurement calculators besides this calculator. Volume conversion does the conversion between different units of measure, but to calculate the volume of a shape, head to our Volume Calculator.

Take a look other related calculators, such as:

What is Volume?

Volume is the space in a three-dimensional world defined by the boundaries or occupied by a particular object. Furthermore, it is a scalar unit, and if we talk about containers, the volume of a container equals its capacity, or in other words, the amount of solid, gas or fluid substance it can contain. For example, you want to calculate how much water you need to refill the bottle or how much gas you need to replenish your car’s gas tank. Therefore, by finding the volume of the container, gas tank, you can figure out everything else. Hence, if a bottle of water is full and contains 1 litre of water, its volume is considered to be 1 l.

How do we calculate the volume of 3D solid shapes? We calculate the volume of solid shapes by dividing them into equal cubical units. Let’s see how we do it:

The volume of a Cuboid

A cuboid is a solid shape of three parts. For example, suppose we have three rectangular planes and stack them one on top of the other. As a result, we will get three parts of the figure: its length, width and height. So, if you multiply all three of them, you will get the formula for calculating the volume of a cuboid.

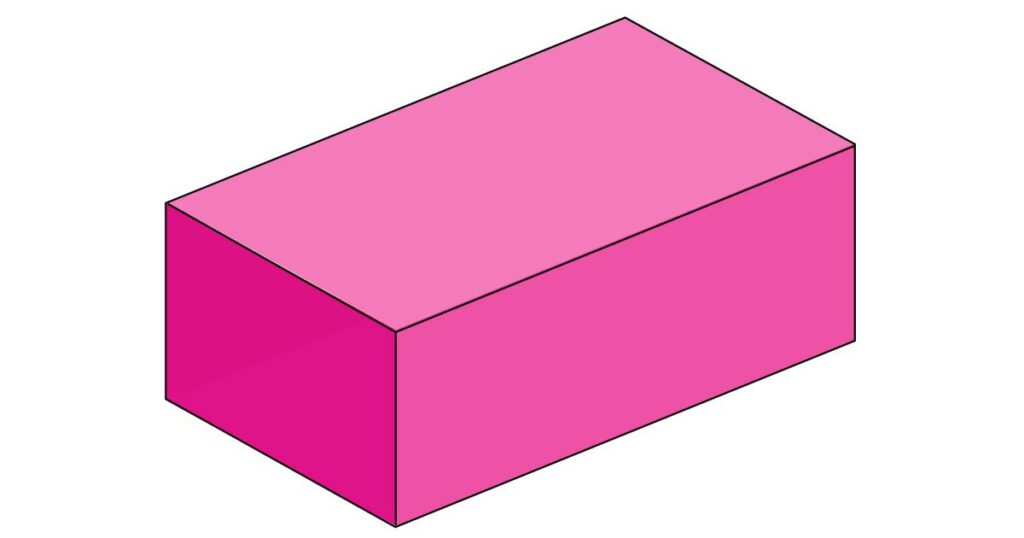
Volume of a cuboid formula: $l \times w \times h$

l – length

w – width

h – height

The volume of a Cube

Cube is a special kind of cuboid. It has three parts, as well, but all the three parts are of equal length. Thus, instead of setting the formula as l x w x h, the formula for the volume of a cube is as follows:

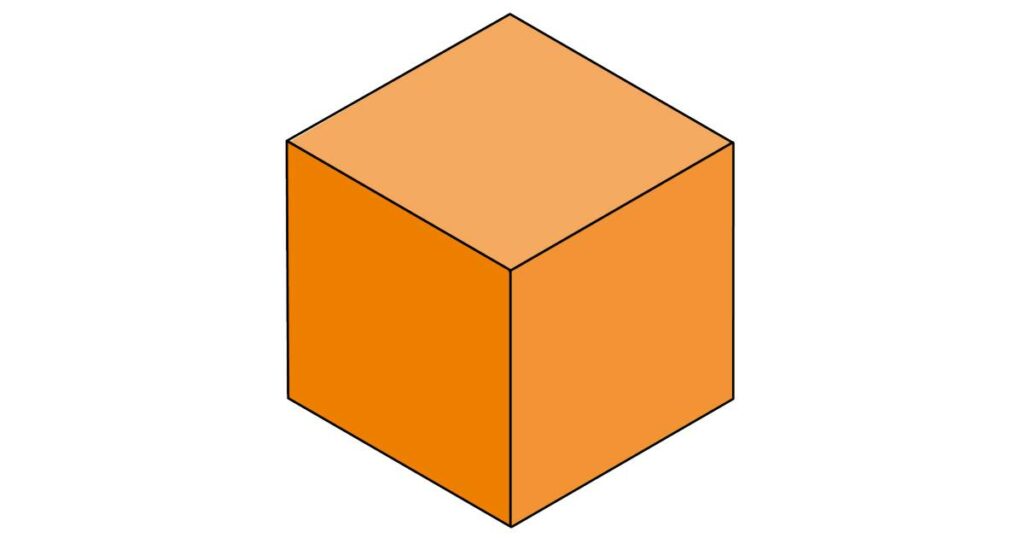
Volume of a cube formula: $a \times a \times a = a^{3}$

The volume of a Cylinder

As you can see, when we talked about cuboids, we said that cuboids are made by stacking a few rectangles on top of each other. The same principle goes with cylinders, but this time with circles, not rectangles. Therefore, if you stack circles, you will get a cylinder. Additionally, every cylinder has two circular bases, the top and the bottom. Every circle has a radius r, so if we combine them, we get the formula of volume of a cylinder as the following:

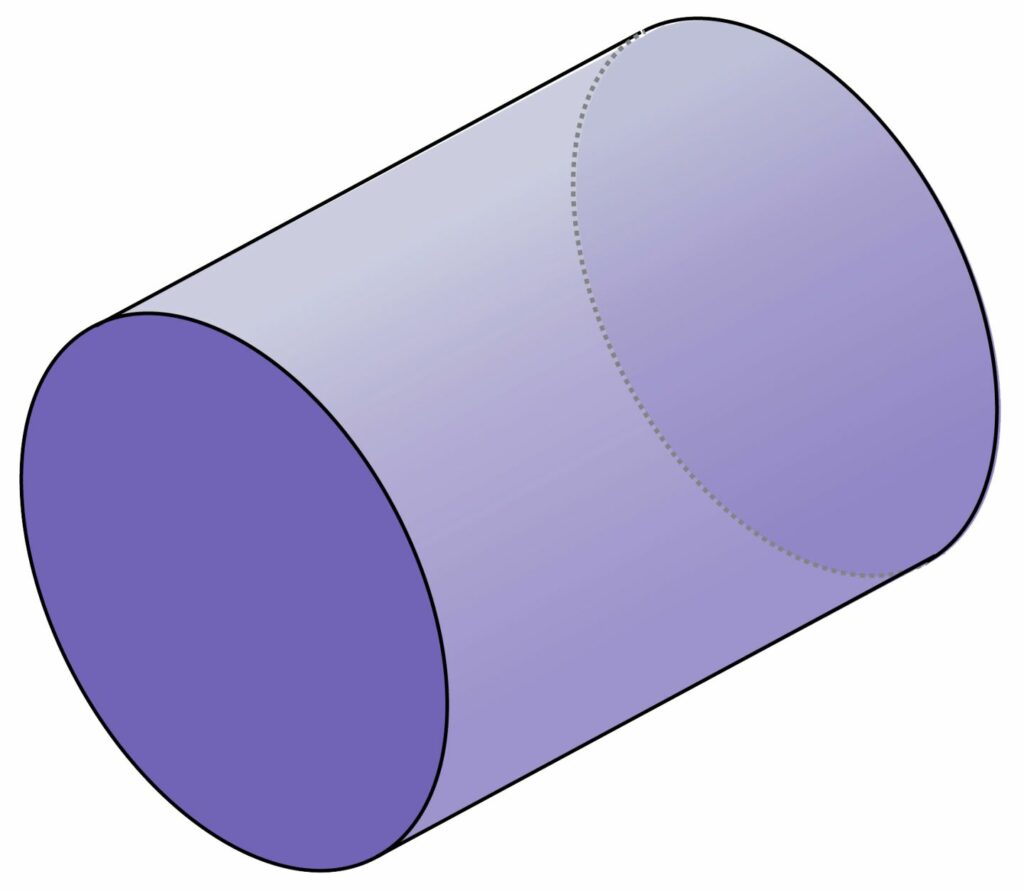
The volume of a cylinder formula: $\pi \times r \times h$

pi – pi number (3,14)

r – radius of each circle (all circles are the same)

h – the distance between the bottom circle and the top one

The volume of a Pyramid

A pyramid is a solid shape structured by two parts: its polygonal base and triangular faces. The polygonal base is made of its length and width. But how do we connect the base with its faces? For instance, we can connect it with the height of the pyramid. The pyramid’s height is the straight line drawn from the centre of its base and the point at which all the triangular faces meet and join. Thus, the formula for finding the volume of a pyramid is the multiplication of its three parts: width, length and height, and once we get that number, we divide it by 3.

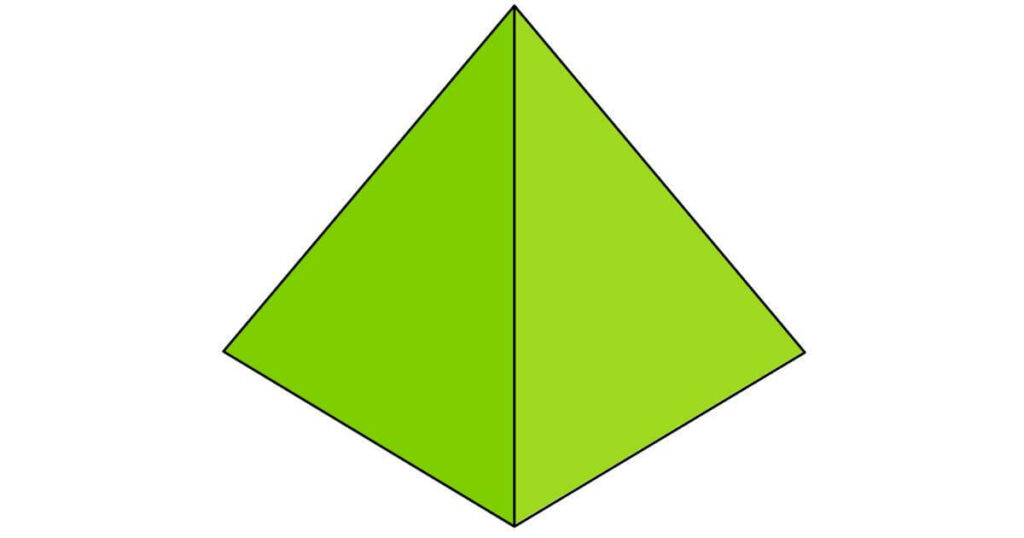
Volume of a pyramid formula: $(l \times w \times h) \div 3$

The volume of a Cone

Cone is a solid shape, very similar to a pyramid, consisting of base and faces. Therefore, the base of a cone is circular, as opposed to the base of a pyramid which is polygonal. The faces of a cone are more rounded as if compared to the ones of a pyramid. For example, if we take into account the length of a circular base’s radius and the height of a cone, we get to the conclusion that the formula of volume of a cone is:

The volume of a cone formula: $\frac{1}{3} \times \pi r 2h$

r – a radius of a circular base

h – the distance between the base and the point where the rounded faces meet

The volume of a Sphere

A sphere is a three-dimensional solid shape for which volume formula you only need to know the length of its radius r. Once you know the radius, you can use the following formula to calculate its volume:

The volume of a sphere formula: $\frac{4}{3} \pi r^{3}$

Meanwhile, check also this Ellipsoid Volume Calculator.

Volume units

The SI (metric measurements system) defines the standard volume unit as m³ or cubic meters. However, other common volume units are:

Litre (L) is the replacement for cubic decimeters (dm³).
Millilitre (mL) is the second name for cubic centimetre (cm³).

Other basic units of volume are presented in the list down below:

1 cubic millimeters (mm³) = 1 mm³
1 cubic centimeter (cm³) = 1 cm³
10 mL= 1 centiliter (cL)
1 milliliter (mL) = 1 mL
10 cL = 1 deciliter (dL)
1 cubic inches (cu in) = 1 (cu in)
1 cubic feet (cu ft) = 1 (cu ft)
10 L = 1 dekaliter (daL)
1 cubic yards (cu yd) = 1 (cu yd)
1 us gallon / uk gallon = 1 (gal)
1000 L= 1 m³
1 quarts (United States) / quarts (United Kingdom) = 1 (US qt or UK qt)
1 imperial pints (United States) / pints (United Kingdom) = 1 (US pt or UK pt)
1000 mL = 1 litre (L)
1 fluid ounces (United States) / fluid ounces (United Kingdom) = 1 (US fl oz / UK fl oz)
1000 cm³= 1 cubic decimeter (dm³)
1 dm³ = 1 litre (L)
10 dL = 1 litre (L)
1 dL = 100 milliliters (mL)
10 daL = 1 hectoliter (hL)
1 hL= 100 litres (L)
1000 L= 1 kilolitre (kL)
1 kL= 10 hectolitre (hL)
15 mL = Eye Drop Bottle
80 mL = Empty Human Stomach
200 mL = Juice Box
355 mL = Soda Pop Can
4L = Full Human Stomach
5 L = Blood in Human Body
235 L = Bathtub
1 ML = Olympic Swimming Pool

Volume conversion chart

There are two ways to express volume: using metric and imperial volume units. However, sometimes you get the volume in one unit, and you want to convert it to another. For instance, you can do it by using a volume conversion chart, which gives you a specific conversion factor that every unit conversion needs. Additionally, there are different metric volume measurements for liquid or gas in different countries. Thus, according to American measurements, standard volume units for liquid are gallons, barrels, quarts or pints. In Great Britain, quarts and pints are also widely used.

You can find conversion value for standard volume units down below:

	milliliter (mL)	liter (L)	cubic meter	cubic inch	cubic feet	pint (pt)	quart (qt)	gallon (gal)	barrel (bbl)
1 milliliter	1	0.001	0.000001	0.061023744094732	0.000035314666721489	0.0021133764188652	0.0010566882094326	0.00026417205235815	0.0000083864143605761
1 liter	1000	1	0.001	61.023744094732	0.035314666721489	2.1133764188652	1.0566882094326	0.26417205235815	0.0083864143605761
1 cubic meter	1000000	1000	1	61023.744094732	35.314666721489	2113.3764188652	1056.6882094326	264.17205235815	8.3864143605761
1 cubic inch	16.387064	0.016387064	0.000016387064	1	0.0005787037037037	0.034632034632035	0.017316017316017	0.0043290043290043	0.00013742870885728
1 cubic feet	28316.846592	28.316846592	0.028316846592	1728	1	59.844155844156	29.922077922078	7.4805194805195	0.23747680890538
1 pint	473.176473	0.473176473	0.000473176473	28.875	0.016710069444444	1	0.5	0.125	0.003968253968254
1 quart	946.352946	0.946352946	0.000946352946	57.75	0.033420138888889	2	1	0.25	0.0079365079365079
1 gallon	3785.411784	3.785411784	0.003785411784	231	0.13368055555556	8	4	1	0.031746031746032
1 barrel	119240.471196	119.240471196	0.119240471196	7276.5	4.2109375	252	126	31.5	1

Volume Conversion Table of Common Volume Units

How to find the volume in a different unit?

When converting volume from one unit to another, you need to use conversion values from the conversion chart table above. For example, we can convert them manually or with the help of our volume calculator. So, let me explain it through a few examples.

Example 1: Convert 20 cubic yards to cubic meters

To convert it, you need to divide the volume by 1.308:

20 / 1.308 = 15.2911 m3

Example 2: Convert 50 cubic inches to US liquid pints

To convert, you need to multiply the volume by 0.034632034632035:

50 x 0.034632034632035 = 1.73 US pt

Volume Conversion