This Class Width Calculator is about calculating the class width of given data. It explains what the calculator is about, its formula, how we should use data in it, and how to find a statistics value – class width. Also, it comes in handy if you want to show your data distribution in a histogram and read more detailed statistics. If you want to know how to use it and read statistics continue reading the article.
Meanwhile, make sure to check our other interesting statistics posts, such as Degrees of Freedom Calculator, Probability of 3 Events Calculator, Chi-Square Calculator or Relative Standard Deviation Calculator. All these calculators can be useful in your everyday life, so don’t hesitate to try them and learn something new or to improve your current knowledge of statistics. Also, there is an interesting calculator for you to learn more about the mean, median and mode, so head to this Mean Median Mode Calculator.
What is class width? – Definition
The class width is defined as the difference between upper and lower, or the minimum and the maximum bounds of class or category. So, to calculate that difference, we have this calculator. It is only valid if all classes have the same width within the distribution.
Class width formula
To estimate the value of the difference between the bounds, the following formula is used:
cw = \frac {max-min} {n}Where:
- max – higher or maximum bound or value;
- min – lower or minimum bound or value;
- n – number of classes within the distribution.
How to use the class width calculator?
After knowing what class width is, the next step is calculating it. Furthermore, to calculate it we use the following steps in this calculator:
- Input the maximum value of the distribution as the “max”,
- Input the minimum value of the distribution as the “min”,
- Enter the number of classes you want for the distribution as “n”,
- Use the given formula to display it.
Example
As an explanation how to calculate class width we are going to use an example of students doing the final exam. Consider that 10 students that have taken the exam and their exam grades are the following: 59, 97, 66, 71, 83, 60, 45, 74, 90, and 56.
- Identify the minimum and the maximum value in the grades data, which are 45 and 97.
- Enter those values in the calculator to calculate the range (the difference between the maximum and the minimum), where we get the result of 52 (max-min = 52)
- To calculate the width, use the number of classes, for example, n = 7.
- The width is returned distributed into 7 classes with it’s formula, where the result is 7.4286. After the result is calculated, it must be rounded up, not rounded off. After rounding up we get 8.
What are the maximum and minimum values?
Maximum and minimum numbers are upper and lower bounds of the given data. From above, we can see that the maximum value is the highest number of all the given numbers, and the minimum value is the lowest number of all the given numbers. Also, for maximum and minimum values, we can show an example of human height.
Let’s compare the heights of 4 basketball players. Their heights are 229, 195, 201, and 210 cm. The maximum value equals the highest number, which is 229 cm, so the max is 229. The same goes with the minimum value, which is 195.
What to do with the class width parameter?
The class width is crucial to representing data as a histogram. The range of it can be divided into several classes. It is useful to arrange the data into its classes to find the frequency of occurrence of values within the set. Given data can be anything.
Having the frequency of occurrence, we can apply it to make a histogram to see its statistics, where the number of classes becomes the number of bars, and class width is the difference between the bar limits.
Class width histogram
A histogram is similar to a bar chart, but the area of the bar shows the frequency of the data. Although the main purpose for a histogram is when the data in groups are not of equal width.
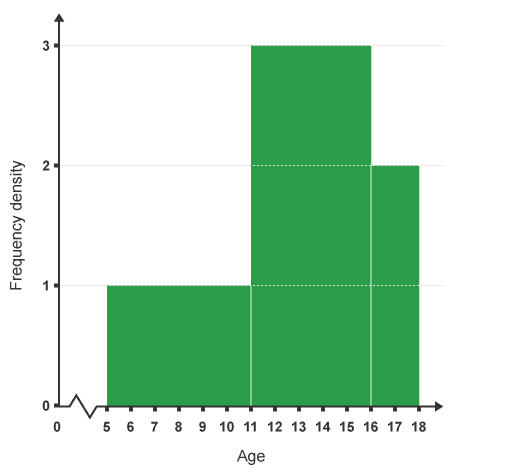
As an example, let’s use the table that shows the ages of 25 children on a trip:
| Age | Frequency | Class width | Frequency density |
| 5-10 | 6 | 6 | 6÷6=1 |
| 11-15 | 15 | 5 | 15÷5=3 |
| 16-17 | 4 | 2 | 4÷2=2 |
In the table, we can see that there are 3 different classes. We call them unequal class intervals. For drawing a histogram with this data, first, we need to find the class width for each of those classes.
After finding it, we need to find the height of the bar or frequency density. To find the frequency density just divide the frequency by the width. After we know the frequency density we can draw a histogram and see its statistics.
FAQ
How do you find the class width?
Determine the min and max values, or limits, the amount of classes, insert them into the formula, and calculate it, or you can try with our calculator instead.
What is the class width example?
As an example, there is calculating the width of the grades from the final exam. After dividing the contrast between the max and min value by the number of classes we get class width.
How do you find frequency values?
Frequency is the number of times some data value occurs. For example, if 3 students score 100 points on a particular exam, then the frequency is 3. Frequency can be represented by f.
What is the class width of class 5 10?
The width of class 5 10 is 10 – 5 = 5.
What are class size and class width?
Both of them are the same, they are the contrast between higher and lower boundaries.
